6.3 Logarithmic Functions Do todos
Learning Objectives
After completing this section, you should be able to…
- Convert from logarithmic to exponential form.
- Convert from exponential to logarithmic form.
- Evaluate logarithms.
- Use common logarithms.
- Use natural logarithms.
In 2010, a major earthquake struck Haiti, destroying or damaging over 285,000 homes. One year later, another, stronger earthquake devastated Honshu, Japan, destroying or damaging over 332,000 buildings, like those shown in Figure 1. Even though both caused substantial damage, the earthquake in 2011 was 100 times stronger than the earthquake in Haiti. How do we know? The magnitudes of earthquakes are measured on a scale known as the Richter Scale. The Haitian earthquake registered a 7.0 on the Richter Scale whereas the Japanese earthquake registered a 9.0.
The Richter Scale is a base-ten logarithmic scale. In other words, an earthquake of magnitude 8 is not twice as great as an earthquake of magnitude 4. It is ![]() times as great! In this lesson, we will investigate the nature of the Richter Scale and the base-ten function upon which it depends.
times as great! In this lesson, we will investigate the nature of the Richter Scale and the base-ten function upon which it depends.
Converting from Logarithmic to Exponential Form
In order to analyze the magnitude of earthquakes or compare the magnitudes of two different earthquakes, we need to be able to convert between logarithmic and exponential form. For example, suppose the amount of energy released from one earthquake were 500 times greater than the amount of energy released from another. We want to calculate the difference in magnitude. The equation that represents this problem is ![]() where
where ![]() represents the difference in magnitudes on the Richter Scale. How would we solve for
represents the difference in magnitudes on the Richter Scale. How would we solve for ![]()
We have not yet learned a method for solving exponential equations. None of the algebraic tools discussed so far is sufficient to solve ![]() We know that
We know that ![]() and
and ![]() so it is clear that
so it is clear that ![]() must be some value between 2 and 3, since
must be some value between 2 and 3, since ![]() is increasing. We can examine a graph, as in Figure 2, to better estimate the solution.
is increasing. We can examine a graph, as in Figure 2, to better estimate the solution.
Estimating from a graph, however, is imprecise. To find an algebraic solution, we must introduce a new function. Observe that the graph in Figure 2 passes the horizontal line test. The exponential function ![]() is one-to-one, so its inverse,
is one-to-one, so its inverse, ![]() is also a function. As is the case with all inverse functions, we simply interchange
is also a function. As is the case with all inverse functions, we simply interchange ![]() and
and ![]() and solve for
and solve for ![]() to find the inverse function. To represent
to find the inverse function. To represent ![]() as a function of
as a function of ![]() we use a logarithmic function of the form
we use a logarithmic function of the form ![]() The base
The base ![]() logarithm of a number is the exponent by which we must raise
logarithm of a number is the exponent by which we must raise ![]() to get that number.
to get that number.
We read a logarithmic expression as, “The logarithm with base ![]() of
of ![]() is equal to
is equal to ![]() ” or, simplified, “log base
” or, simplified, “log base ![]() of
of ![]() is
is ![]() ” We can also say, “
” We can also say, “![]() raised to the power of
raised to the power of ![]() is
is ![]() ” because logs are exponents. For example, the base 2 logarithm of 32 is 5, because 5 is the exponent we must apply to 2 to get 32. Since
” because logs are exponents. For example, the base 2 logarithm of 32 is 5, because 5 is the exponent we must apply to 2 to get 32. Since ![]() we can write
we can write ![]() We read this as “log base 2 of 32 is 5.”
We read this as “log base 2 of 32 is 5.”
We can express the relationship between logarithmic form and its corresponding exponential form as follows:
![]()
Note that the base ![]() is always positive.
is always positive.
Because logarithm is a function, it is most correctly written as ![]() using parentheses to denote function evaluation, just as we would with
using parentheses to denote function evaluation, just as we would with ![]() However, when the input is a single variable or number, it is common to see the parentheses dropped and the expression written without parentheses, as
However, when the input is a single variable or number, it is common to see the parentheses dropped and the expression written without parentheses, as ![]() Note that many calculators require parentheses around the
Note that many calculators require parentheses around the ![]()
We can illustrate the notation of logarithms as follows:
Notice that, comparing the logarithm function and the exponential function, the input and the output are switched. This means ![]() and
and ![]() are inverse functions.
are inverse functions.
Definition of the Logarithmic Function
A logarithm base 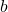 of a positive number
of a positive number 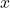 satisfies the following definition.
satisfies the following definition.
For 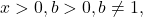
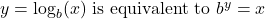 where,
where,
-
we read
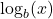 as, “the logarithm with base
as, “the logarithm with base 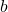 of
of 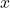 ” or the “log base
” or the “log base 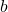 of
of 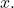 “
“ -
the logarithm
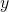 is the exponent to which
is the exponent to which 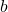 must be raised to get
must be raised to get 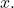
Also, since the logarithmic and exponential functions switch the ![]() and
and ![]() values, the domain and range of the exponential function are interchanged for the logarithmic function. Therefore,
values, the domain and range of the exponential function are interchanged for the logarithmic function. Therefore,
- the domain of the logarithm function with base
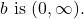
- the range of the logarithm function with base
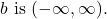
Q&A
Can we take the logarithm of a negative number?
No. Because the base of an exponential function is always positive, no power of that base can ever be negative. We can never take the logarithm of a negative number. Also, we cannot take the logarithm of zero. Calculators may output a log of a negative number when in complex mode, but the log of a negative number is not a real number.
How To
Given an equation in logarithmic form ![]() convert it to exponential form.
convert it to exponential form.
- Examine the equation
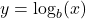 and identify
and identify 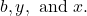
- Rewrite
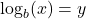 as
as 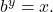
Example 1
Converting from Logarithmic Form to Exponential Form
Write the following logarithmic equations in exponential form.
Solution
First, identify the values of ![]() Then, write the equation in the form
Then, write the equation in the form ![]()
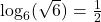 Here,
Here, 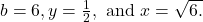 Therefore, the equation
Therefore, the equation 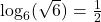 is equivalent to
is equivalent to 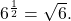
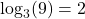 Here,
Here, 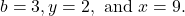 Therefore, the equation
Therefore, the equation 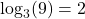 is equivalent to
is equivalent to 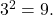
Try It 1
Write the following logarithmic equations in exponential form.
Show Solution
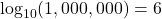 is equivalent to
is equivalent to 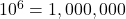
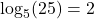 is equivalent to
is equivalent to 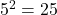
Converting from Exponential to Logarithmic Form
To convert from exponents to logarithms, we follow the same steps in reverse. We identify the base ![]() exponent
exponent ![]() and output
and output ![]() Then we write
Then we write ![]()
Example 2
Converting from Exponential Form to Logarithmic Form
Write the following exponential equations in logarithmic form.
Solution
First, identify the values of ![]() Then, write the equation in the form
Then, write the equation in the form ![]()
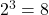 Here,
Here, 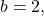
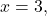 and
and 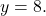 Therefore, the equation
Therefore, the equation 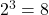 is equivalent to
is equivalent to 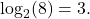
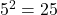 Here,
Here, 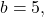
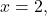 and
and 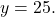 Therefore, the equation
Therefore, the equation 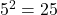 is equivalent to
is equivalent to 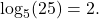
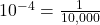 Here,
Here, 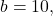
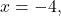 and
and 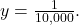 Therefore, the equation
Therefore, the equation 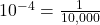 is equivalent to
is equivalent to 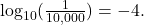
Try It 2
Write the following exponential equations in logarithmic form.
Show Solution
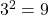 is equivalent to
is equivalent to 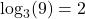
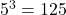 is equivalent to
is equivalent to 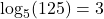
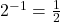 is equivalent to
is equivalent to 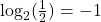
Evaluating Logarithms
Knowing the squares, cubes, and roots of numbers allows us to evaluate many logarithms mentally. For example, consider ![]() We ask, “To what exponent must
We ask, “To what exponent must ![]() be raised in order to get 8?” Because we already know
be raised in order to get 8?” Because we already know ![]() it follows that
it follows that ![]()
Now consider solving ![]() and
and ![]() mentally.
mentally.
- We ask, “To what exponent must 7 be raised in order to get 49?” We know
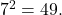 Therefore,
Therefore, 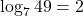
- We ask, “To what exponent must 3 be raised in order to get 27?” We know
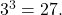 Therefore,
Therefore, 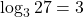
Even some seemingly more complicated logarithms can be evaluated without a calculator. For example, let’s evaluate ![]() mentally.
mentally.
- We ask, “To what exponent must
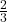 be raised in order to get
be raised in order to get 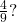 ” We know
” We know 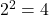 and
and 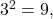 so
so 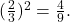 Therefore,
Therefore, 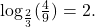
How To
Given a logarithm of the form ![]() evaluate it mentally.
evaluate it mentally.
- Rewrite the argument
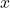 as a power of
as a power of 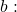
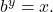
- Use previous knowledge of powers of
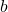 identify
identify 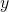 by asking, “To what exponent should
by asking, “To what exponent should 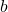 be raised in order to get
be raised in order to get 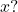 ”
”
Example 3
Solving Logarithms Mentally
Solve ![]() without using a calculator.
without using a calculator.
Solution
First we rewrite the logarithm in exponential form: ![]() Next, we ask, “To what exponent must 4 be raised in order to get 64?”
Next, we ask, “To what exponent must 4 be raised in order to get 64?”
We know ![]()
Therefore, ![]()
Try It 3
Solve ![]() without using a calculator.
without using a calculator.
Show Solution
Example 4
Evaluating the Logarithm of a Reciprocal
Evaluate ![]() without using a calculator.
without using a calculator.
Solution
First we rewrite the logarithm in exponential form: ![]() Next, we ask, “To what exponent must 3 be raised in order to get
Next, we ask, “To what exponent must 3 be raised in order to get ![]() ”
”
We know ![]() but what must we do to get the reciprocal,
but what must we do to get the reciprocal, ![]() Recall from working with exponents that
Recall from working with exponents that ![]() We use this information to write
We use this information to write
![]()
Therefore, ![]()
Try It 4
Evaluate ![]() without using a calculator.
without using a calculator.
Show Solution
Using Common Logarithms
Sometimes you may see a logarithm written without a base. When you see one written this way, you need to look at the expression before evaluating it. It may be that the base you use doesn’t matter. If you find it in computer science, it often means ![]() . However, in mathematics it almost always means the common logarithm of 10. In other words, the expression
. However, in mathematics it almost always means the common logarithm of 10. In other words, the expression ![]() often means
often means ![]()
Definition of the Common Logarithm
A common logarithm is a logarithm with base 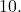 We can also write
We can also write 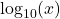 simply as
simply as 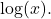 The common logarithm of a positive number
The common logarithm of a positive number 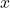 satisfies the following definition.
satisfies the following definition.
For 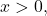
We read 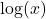 as, “the logarithm with base
as, “the logarithm with base 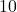 of
of 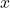 ” or “log base 10 of
” or “log base 10 of 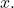 ”
”
The logarithm 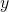 is the exponent to which
is the exponent to which 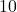 must be raised to get
must be raised to get 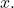
Currently, we use ![]() as the common logarithm,
as the common logarithm, ![]() as the binary logarithm, and
as the binary logarithm, and ![]() as the natural logarithm. Writing
as the natural logarithm. Writing ![]() without specifying a base is now considered bad form, despite being frequently found in older materials.
without specifying a base is now considered bad form, despite being frequently found in older materials.
How To
Given a common logarithm of the form ![]() evaluate it mentally.
evaluate it mentally.
- Rewrite the argument
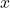 as a power of
as a power of 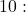
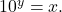
- Use previous knowledge of powers of
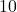 to identify
to identify 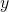 by asking, “To what exponent must
by asking, “To what exponent must 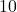 be raised in order to get
be raised in order to get 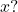 ”
”
Example 5
Finding the Value of a Common Logarithm Mentally
Evaluate ![]() without using a calculator.
without using a calculator.
Solution
First we rewrite the logarithm in exponential form: ![]() Next, we ask, “To what exponent must
Next, we ask, “To what exponent must ![]() be raised in order to get 1000?” We know
be raised in order to get 1000?” We know
![]()
Therefore, ![]()
Try It 5
Evaluate ![]()
Show Solution
How To
Given a common logarithm with the form ![]() evaluate it using a calculator.
evaluate it using a calculator.
- Press [LOG].
- Enter the value given for
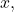 followed by [ ) ].
followed by [ ) ]. - Press [ENTER].
Example 6
Finding the Value of a Common Logarithm Using a Calculator
Evaluate ![]() to four decimal places using a calculator.
to four decimal places using a calculator.
Solution
- Press [LOG].
- Enter 321, followed by [ ) ].
- Press [ENTER].
Rounding to four decimal places, ![]()
Analysis
Note that ![]() and that
and that ![]() Since 321 is between 100 and 1000, we know that
Since 321 is between 100 and 1000, we know that ![]() must be between
must be between ![]() and
and ![]() This gives us the following:
This gives us the following:
![]()
Try It 6
Evaluate ![]() to four decimal places using a calculator.
to four decimal places using a calculator.
Show Solution
Example 7
Rewriting and Solving a Real-World Exponential Model
The amount of energy released from one earthquake was 500 times greater than the amount of energy released from another. The equation ![]() represents this situation, where
represents this situation, where ![]() is the difference in magnitudes on the Richter Scale. To the nearest thousandth, what was the difference in magnitudes?
is the difference in magnitudes on the Richter Scale. To the nearest thousandth, what was the difference in magnitudes?
Solution
We begin by rewriting the exponential equation in logarithmic form.
![]()
Next we evaluate the logarithm using a calculator:
- Press [LOG].
- Enter
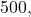 followed by [ ) ].
followed by [ ) ]. - Press [ENTER].
- To the nearest thousandth,
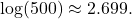
The difference in magnitudes was about ![]()
Try It 7
The amount of energy released from one earthquake was ![]() times greater than the amount of energy released from another. The equation
times greater than the amount of energy released from another. The equation ![]() represents this situation, where
represents this situation, where ![]() is the difference in magnitudes on the Richter Scale. To the nearest thousandth, what was the difference in magnitudes?
is the difference in magnitudes on the Richter Scale. To the nearest thousandth, what was the difference in magnitudes?
Show Solution
Using Natural Logarithms
The most frequently used base for logarithms is ![]() the value of which is approximately
the value of which is approximately ![]() . Base
. Base ![]() logarithms are important in calculus and some scientific applications; they are called natural logarithms. The base
logarithms are important in calculus and some scientific applications; they are called natural logarithms. The base ![]() logarithm,
logarithm, ![]() has its own notation,
has its own notation, ![]()
Most values of ![]() can be found only using a calculator. The major exception is that, because the logarithm of 1 is always 0 in any base,
can be found only using a calculator. The major exception is that, because the logarithm of 1 is always 0 in any base, ![]() For other natural logarithms, we can use the
For other natural logarithms, we can use the ![]() key that can be found on most scientific calculators. We can also find the natural logarithm of any power of
key that can be found on most scientific calculators. We can also find the natural logarithm of any power of ![]() using the inverse property of logarithms.
using the inverse property of logarithms.
Definition of the Natural Logarithm
A natural logarithm is a logarithm with base 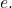 We write
We write 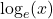 simply as
simply as 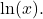 The natural logarithm of a positive number
The natural logarithm of a positive number 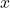 satisfies the following definition.
satisfies the following definition.
For 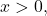
We read 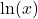 as, “the logarithm with base
as, “the logarithm with base  of
of 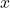 ” or “the natural logarithm of
” or “the natural logarithm of 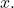 ”
”
The logarithm 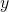 is the exponent to which
is the exponent to which  must be raised to get
must be raised to get 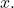
Since the functions 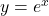 and
and 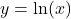 are inverse functions,
are inverse functions, 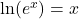 for all
for all 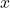 and
and 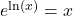 for
for 
How To
Given a natural logarithm with the form ![]() evaluate it using a calculator.
evaluate it using a calculator.
- Press [LN].
- Enter the value given for
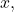 followed by [ ) ].
followed by [ ) ]. - Press [ENTER].
Example 8
Evaluating a Natural Logarithm Using a Calculator
Evaluate ![]() to four decimal places using a calculator.
to four decimal places using a calculator.
Solution
- Press [LN].
- Enter
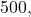 followed by [ ) ].
followed by [ ) ]. - Press [ENTER].
Rounding to four decimal places, ![]()
Try It 8
Evaluate ![]()
Show Solution
6.3 Exercise Set
- What is a base
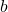 logarithm? Discuss the meaning by interpreting each part of the equivalent equations
logarithm? Discuss the meaning by interpreting each part of the equivalent equations 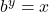 and
and 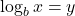 for
for 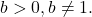
- How is the logarithmic function
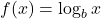 related to the exponential function
related to the exponential function 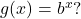 What is the result of composing these two functions?
What is the result of composing these two functions? - How can the logarithmic equation
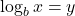 be solved for
be solved for 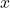 using the properties of exponents?
using the properties of exponents? - Discuss the meaning of the common logarithm. What is its relationship to a logarithm with base
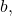 and how does the notation differ?
and how does the notation differ? - Discuss the meaning of the natural logarithm. What is its relationship to a logarithm with base
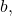 and how does the notation differ?
and how does the notation differ? 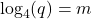
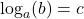
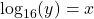
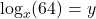
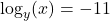
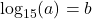
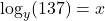
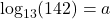
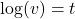
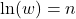
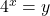
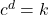
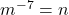
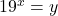
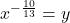
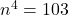
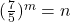
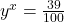
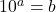
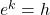
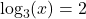
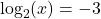
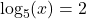
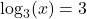
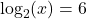
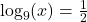
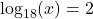
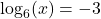
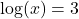
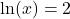
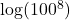
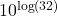
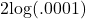
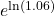
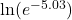
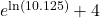
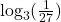
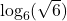
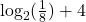
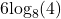
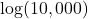
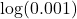
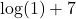
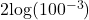
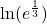
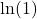
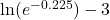
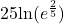
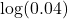
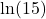
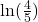
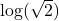
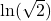
- Is
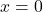 in the domain of the function
in the domain of the function 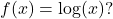 If so, what is the value of the function when
If so, what is the value of the function when 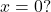 Verify the result.
Verify the result. - Is
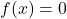 in the range of the function
in the range of the function 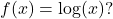 If so, for what value of
If so, for what value of 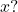 Verify the result.
Verify the result. - Is there a number
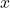 such that
such that 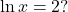 If so, what is that number? Verify the result.
If so, what is that number? Verify the result. - Is the following true:
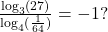 Verify the result.
Verify the result. - Is the following true:
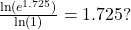 Verify the result.
Verify the result. - The exposure index
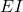 for a camera is a measurement of the amount of light that hits the image receptor. It is determined by the equation
for a camera is a measurement of the amount of light that hits the image receptor. It is determined by the equation 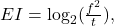 where
where 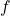 is the “f-stop” setting on the camera, and
is the “f-stop” setting on the camera, and 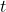 is the exposure time in seconds. Suppose the f-stop setting is
is the exposure time in seconds. Suppose the f-stop setting is 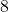 and the desired exposure time is
and the desired exposure time is 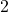 seconds. What will the resulting exposure index be?
seconds. What will the resulting exposure index be? - Refer to the previous exercise. Suppose the light meter on a camera indicates an
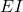 of
of 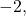 and the desired exposure time is 16 seconds. What should the f-stop setting be?
and the desired exposure time is 16 seconds. What should the f-stop setting be? - The intensity levels I of two earthquakes measured on a seismograph can be compared by the formula
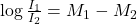 where
where 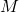 is the magnitude given by the Richter Scale. In August 2009, an earthquake of magnitude 6.1 hit Honshu, Japan. In March 2011, that same region experienced yet another, more devastating earthquake, this time with a magnitude of 9.0. How many times greater was the intensity of the 2011 earthquake? Round to the nearest whole number.
is the magnitude given by the Richter Scale. In August 2009, an earthquake of magnitude 6.1 hit Honshu, Japan. In March 2011, that same region experienced yet another, more devastating earthquake, this time with a magnitude of 9.0. How many times greater was the intensity of the 2011 earthquake? Round to the nearest whole number.
#TODO: Add in the answers from https://openstax.org/books/algebra-and-trigonometry-2e/pages/6-3-logarithmic-functions
Text Attribution
This text was adapted from Chapter 6.3 of Algebra and Trigonometry 2e, textbooks originally published by OpenStax.
