Answer Key Chapter 6 – Contemporary Mathematics | OpenStax
Try It 6.1
-
To write n% in its fractional form is to write the percent as the fraction
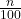 .
.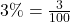
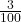
-
To write n% in its fractional form is to write the percent as the fraction
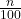 .
.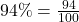
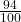
-
To write n% in its fractional form is to write the percent as the fraction
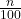 .
.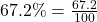
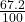
-
To write n% in its fractional form is to write the percent as the fraction
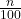 .
.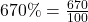
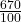
Try It 6.2
-
The decimal form of n% is found by calculating the decimal value of n ÷ 100.
9% is 9 divided by 100.
This moves the decimal point two places to the left, resulting in 0.09.
0.09
-
The decimal form of n% is found by calculating the decimal value of n ÷ 100.
24% is 24 divided by 100.
This moves the decimal point two places to the left, resulting in 0.24.
0.24
-
The decimal form of n% is found by calculating the decimal value of n ÷ 100.
2.18% is 2.18 divided by 100.
This moves the decimal point two places to the left, resulting in 0.0218.
0.0218
Try It 6.3
-
To convert the number x from decimal form to percent, multiply x by 100 and place a percent sign, %, after the number:
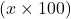 .
.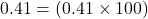
41%
-
To convert the number x from decimal form to percent, multiply x by 100 and place a percent sign, %, after the number:
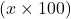 .
.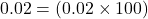
2%
-
To convert the number x from decimal form to percent, multiply x by 100 and place a percent sign, %, after the number:
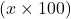 .
.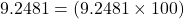
924.81%
Try It 6.4
-
The formula relating the total (base), the percent in decimal form, and the part (amount) is
 or
or 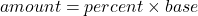 .
.26% of 1,300

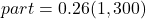
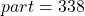
338
-
The formula relating the total (base), the percent in decimal form, and the part (amount) is
 or
or 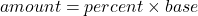 .
.225% of 915

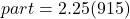
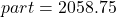
2058.75
Try It 6.5
-
The formula relating the total (base), the percent in decimal form, and the part (amount) is
 .
.45 is 18% of the total.
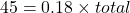
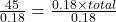
The total is 250.
250
-
The formula relating the total (base), the percent in decimal form, and the part (amount) is
 .
.900 is 15% of the total.
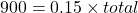
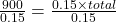
The total is 6,000.
6,000
Try It 6.6
-
The formula relating the total (base), the percent in decimal form, and the part (amount) is
 .
.25 is what percent of 40?
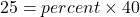
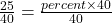
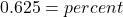
To convert the number x from decimal form to percent, multiply x by 100 and place a percent sign, %, after the number: (x × 100)%.
0.625 = 62.5%
62.5%
-
The formula relating the total (base), the percent in decimal form, and the part (amount) is
 .
.292 is what percent of 730?
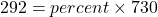
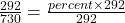
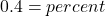
To convert the number x from decimal form to percent, multiply x by 100 and place a percent sign, %, after the number: (x × 100)%.
0.40 = 40%
40%
Try It 6.7
-
The formula relating the total (base), the percent in decimal form, and the part (amount) is
 or
or 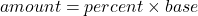 .
.30% of $1,765

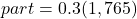
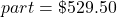
The amount is $529.50.
$529.50
Try It 6.8
-
The formula relating the total (base), the percent in decimal form, and the part (amount) is
 .
.1,679 is what percent of 2,532?
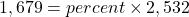
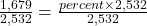
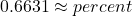
To convert the number x from decimal form to percent, multiply x by 100 and place a percent sign, %, after the number: (x × 100)%.
0.6631 = 66.31%
66.31%
Try It 6.9
-
The formula relating the total (base), the percent in decimal form, and the part (amount) is
 .
.52 is 65% of the total.
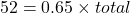
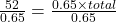
The total is 80 bulbs.
80 bulbs.
Try It 6.10
-
discount = percent discount × original price
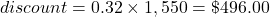
sale price = original price – discount
sale price = 1,550 – 496 = $1,054
The discount is $496 and the sale price is $1,054.
Discount is $496; sale price is $1,054.00
-
discount = percent discount × original price
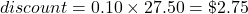
sale price = original price – discount
sale price = 27.50 – 2.75 = $24.75
The discount is $2.75 and the sale price is $24.75.
Discount is $2.75; sale price is $24.75
Try It 6.11
-
35%
sale price = original price – discount
162.50 = 250 – discount
discount = 87.50
87.50 is what percent of 250?
87.50 = percent discount × 250
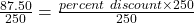
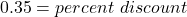
The percent discount is 35%.
-
12%
sale price = original price – discount
17.16 = 19.50 – discount
discount = 2.34
2.34 is what percent of 19.50?
2.34 = percent discount × 19.50
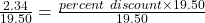
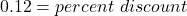
The percent discount is 12%.
Try It 6.12
-
$13.00
If the percent discount was 15%, the sale price is 85% of the original price.
sale price = original price × (1 – percent discount)
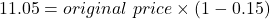
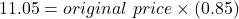
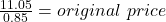
The original price was $13.
-
$220.00
If the percent discount was 9%, the sale price is 91% of the original price.
sale price = original price × (1 – percent discount)
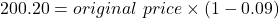
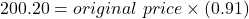
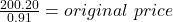
The original price was $220.
Try It 6.13
-
discount = percent discount × original price
discount = 0.60 × 550 = $330
sale price = original price – discount
sale price = 550 – 330 = $220
The discount is $330 and the sale price is $220.
Discount is $330; sale price of the bed is $220.
Try It 6.14
-
sale price = original price – discount
13.43 = 15.80 – discount
discount = 2.37
2.37 is what percent of 15.80?
2.37 = percent discount × 15.80
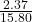 = percent discount
= percent discount0.15 = percent discount
The percent discount is 15%.
15%
Try It 6.15
-
100% – 26% = 74%
If the percent discount was 26%, the sale price is 76% of the original price.
sale price = original price × (1 – percent discount)
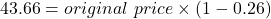
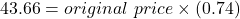
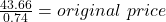
The original price was $59.
$59.00
Try It 6.16
-
markup = percent markup × cost
markup = 0.22 × $1,800
markup = $396
retail price = cost + markup
retail price = 1,800 + 396 = $2,196
Markup is $396; retail price is $2,196.00.
-
markup = percent markup × cost
markup = 0.10 × $10.50
markup = $1.05
retail price = cost + markup
retail price = 10.50 + 1.05 = $11.55
Markup is $1.05; retail price is $11.55.
Try It 6.17
-
retail price = cost + markup
190 = 120 + markup
70 = markup
The markup is what percent of cost?
70 is what percent of 120?
70 = percent markup × 120
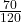 = percent markup
= percent markup0.5833 ≈ percent markup
58.33% ≈ percent markup
58.33%
-
retail price = cost + markup
1.14 = 0.38 + markup
0.76 = markup
The markup is what percent of cost?
0.76 is what percent of 0.38?
0.76 = percent markup × 0.38
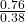 = percent markup
= percent markup2 = percent markup
200% = percent markup
200%
Try It 6.18
-
retail price = cost × (1 + percent markup)
40.25 = cost × (1 + 0.15) 40.25 = cost × (1.15) Divide by 1.15. $35 = cost $35.00
-
retail price = cost × (1 + percent markup)
35.96 = cost × (1 + 3.00) 35.96 = cost × (4) Divide by 4. $8.99 = cost $8.99
Try It 6.19
-
markup = percent markup × cost
markup = 2.50 × 360
markup = 900
retail price = cost + markup
retail price = 360 + 900 = $1,260
The retail price is $1,260.
The retail price of the bed is $1,260.00.
Try It 6.20
-
retail price = cost + markup
234.36 = 189 + markup Subtract 189. 45.36 = markup
The markup is what percent of cost?
45.36 is what percent of 189?
45.36 = percent markup × 189
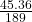 = percent markup
= percent markup0.24 = percent markup
24% = percent markup
The percent markup is 24 percent.
24%
Try It 6.21
-
retail price = cost × (1 + percent markup)
57 = cost × (1 + 0.50) 57 = cost × (1.5) Divide by 1.5. $38 = cost Tina’s cost is $38. $38.00
Try It 6.22
-
sales tax = purchase price × tax rate
sales tax = 1,499 × 0.07
sales tax = $104.93
total price = purchase price + sales tax = 1,499 + 104.93 = $1,603.93
The sales tax is $104.93 and the total price is $1,603.93.
Sales tax is $104.93; total price is $1,603.93.
-
sales tax = purchase price × tax rate
sales tax = 26.89 × 0.07
sales tax = $1.88 (rounded to the nearest cent) total price = purchase price + sales tax = 26.89 + 1.88 = $28.77
The sales tax is $1.88 and the total price is $28.77.
Sales tax is $1.88; total price is $28.77.
Try It 6.23
-
total price = purchase price + sales tax
88.30 = 83.90 + sales tax
$4.40 = sales tax
sales tax = purchase price × tax rate
4.40 = 83.90 × tax rate
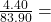 tax rate
tax rate0.052443… ≈ tax rate
The tax rate is approximately 5.24%.
Sales tax rate = 5.25%
-
total price = purchase price + sales tax
509.20 = 477 + sales tax
$32.20 = sales tax
sales tax = purchase price × tax rate
32.20 = 477 × tax rate
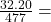 tax rate
tax rate0.0675 ≈ tax rate
The tax rate is approximately 6.75%.
Sales tax rate = 6.75%
Try It 6.24
-
total price = purchase price × (1 + tax rate)
157.81 = purchase price × (1 + 0.0825)
157.81 = purchase price × (1.0825)
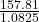 = purchase price
= purchase price$145.78 ≈ purchase price (rounded to the nearest cent) $145.78
-
total price = purchase price × (1 + tax rate)
522.01 = purchase price × (1 + 0.0675)
522.01 = purchase price × (1.0675)
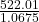 = purchase price
= purchase price$489.00 ≈ purchase price (rounded to the nearest cent) $489.00
Try It 6.25
-
sales tax = purchase price × tax rate
sales tax = 1,149 × 0.0968
sales tax = $111.22 (rounded to the nearest cent) total price = purchase price + sales tax = 1,149 + 111.22 = $1,260.22
Daryl’s sales tax is $111.22. The total price is $1,260.22.
Sales tax is $111.22. The total price Daryl pays is $1,260.22.
Try It 6.26
-
total price = purchase price × (1 + tax rate)
153 = purchase price × (1 + 0.0625)
153 = purchase price × (1.0625)
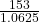 = purchase price
= purchase price$144 = purchase price
total price = purchase price + sales tax
153 = 144 + sales tax
$9 = sales tax
The sales tax is $9.
The sales tax is $9.
Try It 6.27
-
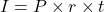
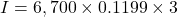
The interest is $2,409.99.
The loan payoff is the sum of the principal and the interest.
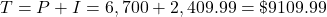
Interest = $2,409.99, the loan payoff is $9,109.99
-
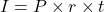
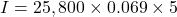
The interest is $8,901.
The loan payoff is the sum of the principal and the interest.
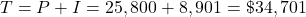
Interest = $8,901, the loan payoff is $34,701.00
Try It 6.28
-
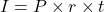
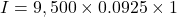
The interest is $878.75.
The loan payoff is the sum of the principal and the interest.
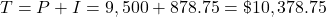
The total repayment is $10,378.75.
She will pay $878.75 in interest, total repayment is $10,378.75.
Try It 6.29
-
Remember that 6 months is 0.5 years.
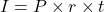
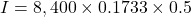
The interest is $727.86.
The loan payoff is the sum of the principal and the interest.
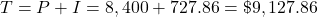
The payoff is $9,127.86.
He will pay $727.86 in interest, payoff is $9,127.86.
Try It 6.30
-
Remember that 60 days is
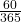 years.
years.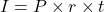
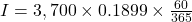
The interest is $115.51 (rounded to the nearest cent; interest is usually rounded up when paid to the lender).
The loan payoff is the sum of the principal and the interest.
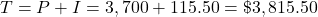
The loan payoff is $3,815.50.
The cost to borrow is $115.51 and their payoff is $3,815.51.
Try It 6.31
-
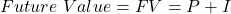
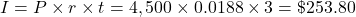
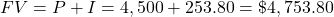
Interest = $253.8, FV = $4,753.80
-
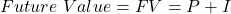
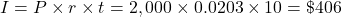
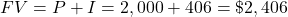
Interest = $406.00, FV = $2,406.00
-
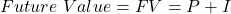
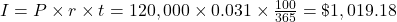
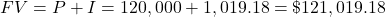
Interest= $1019.18, FV = $121,019.18
-
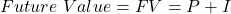
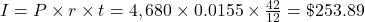
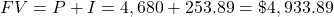
Interest = $253.89, FV = $4,933.89
Try It 6.32
-
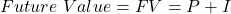
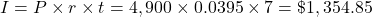
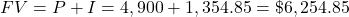
Mia will receive $6,254.85.
Try It 6.33
-
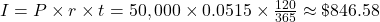
(rounded to the nearest cent) $846.58
-
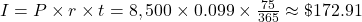
(rounded to the nearest cent) $172.91
Try It 6.34
-
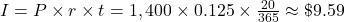
(rounded to the nearest cent) Subtract the interest off the loan payment.
$700 – 9.59 = $690.41 went toward paying off the loan.
$1,400 – 690.41 = $709.59 is the remaining balance of the loan.
$709.59
-
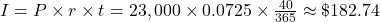
(rounded to the nearest cent) Subtract the interest off the loan payment.
$10,000 – 182.74 = $9,817.26 went toward paying off the loan.
$23,000 – 9,817.26 = $13,182.74 is the remaining balance of the loan.
$13,182.74
Try It 6.35
-
Interest on the loan after 75 days:
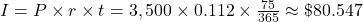
Interest on the loan after 30 days:
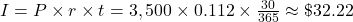 (rounded to the nearest cent)
(rounded to the nearest cent)Subtract the partial interest off the loan payment.
$1,250 – 32.22 = $1,217.78 went toward paying off the loan.
$3,500 – 1217.78 = $2,282.22 is the remaining balance of the loan.
There are 45 more days to pay interest:
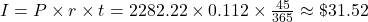 more interest will accrue.
more interest will accrue.The total payout left of the loan is the balance of the loan plus the additional interest.
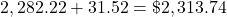
$2,313.74
Try It 6.36
-
The amount of monthly payments, A, for a loan with principal P, monthly simple interest rate r (in decimal form), for t number of months is found using the formula
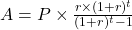 . The monthly interest rate is the annual interest rate divided by 12.
. The monthly interest rate is the annual interest rate divided by 12.5 years = 60 months
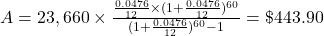
$443.90
Try It 6.37
-
The present value, PV, of money deposited at an annual, simple interest rate of r (in decimal form) for time t (in years) with a specified future value of FV is calculated with the formula
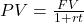 . Present value, in this calculation, is always rounded up. Otherwise, the future value may fall short of the target future value.
. Present value, in this calculation, is always rounded up. Otherwise, the future value may fall short of the target future value.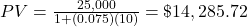
(rounded up to the next cent) $14,285.72 needs to be invested in an account earning 7.5% annual simple interest to have $25,000 at the end of the 10 years.
$14,285.72. $14,285.72 needs to be invested so that, after 10 years at 7.5% interest, the investment will be worth $25,000.
-
The present value, PV, of money deposited at an annual, simple interest rate of r (in decimal form) for time t (in years) with a specified future value of FV is calculated with the formula
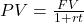 . Present value, in this calculation, is always rounded up. Otherwise, the future value may fall short of the target future value.
. Present value, in this calculation, is always rounded up. Otherwise, the future value may fall short of the target future value.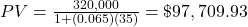
(rounded up to the next cent) $97,709.93 needs to be invested in an account earning 6.5% annual simple interest to have $320,000 at the end of the 35 years.
$97,709.93. $97,709.93 needs to be invested so that, after 35 years at 6.5% interest, the investment will be worth $320,000.
-
The present value, PV, of money deposited at an annual, simple interest rate of r (in decimal form) for time t (in years) with a specified future value of FV is calculated with the formula
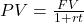 . Present value, in this calculation, is always rounded up. Otherwise, the future value may fall short of the target future value.
. Present value, in this calculation, is always rounded up. Otherwise, the future value may fall short of the target future value.270 months is 22.5 years.
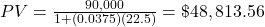
(rounded up to the next cent) $48,813.56 needs to be invested in an account earning 3.75% annual simple interest to have $90,000 at the end of the 22.5 years.
$48,813.56. $48,813.56 needs to be invested so that, after 270 months at 3.75% interest, the investment will be worth $90,000.
Try It 6.38
-
The present value, PV, of money deposited at an annual, simple interest rate of r (in decimal form) for time t (in years) with a specified future value of FV is calculated with the formula
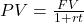 . Present value, in this calculation, is always rounded up. Otherwise, the future value may fall short of the target future value.
. Present value, in this calculation, is always rounded up. Otherwise, the future value may fall short of the target future value.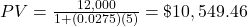
(rounded up to the next cent) $10,549.46
Try It 6.39
-
The interest
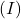 is the principal
is the principal 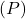 times the annual simple interest rate as a decimal
times the annual simple interest rate as a decimal 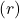 times the time in years
times the time in years 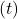 .
.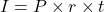
Step 1: End of the first year
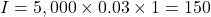
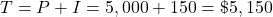
The interest is added into the account and you begin earning interest on $5,150.
Step 2: End of the second year
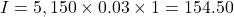
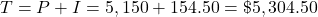
The interest is added into the account and you begin earning interest on $5,304.50.
Step 3: End of the third year
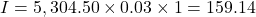
(rounded) 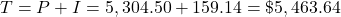
The interest is added into the account and you begin earning interest on $5,463.64.
Step 4: End of the fourth year
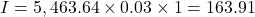
(rounded) 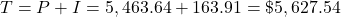
The interest is added into the account and you begin earning interest on $5,627.54.
The CD is worth $5,627.54 after 4 years.
Try It 6.40
-
From the previous exercise, you know she earned $5,627.54 when compounded annually.
Find the amount if earning simple interest:
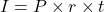
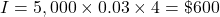
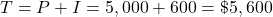
You earned $27.54 more when compounding interest.
CD would have been worth $5,600. Oksana earned $27.54 more with compound interest.
Try It 6.41
-
The future value of an investment,
 , when the principal,
, when the principal, 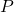 , is invested at an annual interest rate of
, is invested at an annual interest rate of  (in decimal form), compounded
(in decimal form), compounded 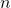 times per year for
times per year for 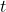 years is found using the formula
years is found using the formula 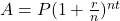 .
.Hint: Find
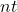 before you plug numbers into your calculator!
before you plug numbers into your calculator! 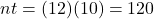 It will help you get the right results. Use those parentheses in your calculator, too!
It will help you get the right results. Use those parentheses in your calculator, too!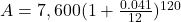
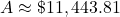
$11,443.81
-
The future value of an investment,
 , when the principal,
, when the principal, 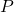 , is invested at an annual interest rate of
, is invested at an annual interest rate of  (in decimal form), compounded
(in decimal form), compounded 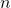 times per year for
times per year for 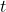 years is found using the formula
years is found using the formula 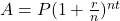 .
.Hint: Find
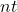 before you plug numbers into your calculator!
before you plug numbers into your calculator! 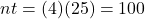 It will help you get the right results. Use those parentheses in your calculator, too!
It will help you get the right results. Use those parentheses in your calculator, too!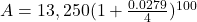
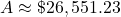
$26,551.23
Try It 6.42
-
The future value of an investment,
 , when the principal,
, when the principal, 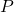 , is invested at an annual interest rate of
, is invested at an annual interest rate of  (in decimal form), compounded
(in decimal form), compounded 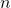 times per year for
times per year for 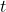 years is found using the formula
years is found using the formula 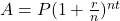 .
.Hint: Find
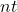 before you plug numbers into your calculator!
before you plug numbers into your calculator! 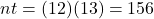 It will help you get the right results. Use those parentheses in your calculator, too!
It will help you get the right results. Use those parentheses in your calculator, too!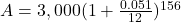
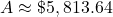
$5,813.64
Try It 6.43
-
The future value of an investment,
 , when the principal,
, when the principal, 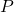 , is invested at an annual interest rate of
, is invested at an annual interest rate of  (in decimal form), compounded
(in decimal form), compounded 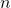 times per year for
times per year for 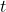 years is found using the formula
years is found using the formula 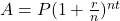 .
.Hint: Find
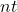 before you plug numbers into your calculator!
before you plug numbers into your calculator! 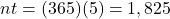 It will help you get the right results. Use those parentheses in your calculator, too!
It will help you get the right results. Use those parentheses in your calculator, too!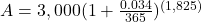
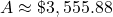
$3,555.88
Try It 6.44
-
The money invested in an account bearing an annual interest rate of
 (in decimal form), compounded
(in decimal form), compounded 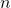 times per year for
times per year for 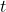 years, is called the present value,
years, is called the present value, 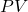 , of the account (or of the money) and found using the formula
, of the account (or of the money) and found using the formula 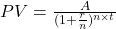 where
where  is the value of the account at the investment’s end. Always round this value up to the next penny.
is the value of the account at the investment’s end. Always round this value up to the next penny.Hint: Find
 before you plug numbers into your calculator!
before you plug numbers into your calculator! 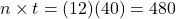
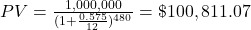
$100,811.07
-
The money invested in an account bearing an annual interest rate of
 (in decimal form), compounded
(in decimal form), compounded 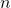 times per year for
times per year for 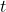 years, is called the present value,
years, is called the present value, 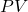 , of the account (or of the money) and found using the formula
, of the account (or of the money) and found using the formula 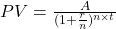 where
where  is the value of the account at the investment’s end. Always round this value up to the next penny.
is the value of the account at the investment’s end. Always round this value up to the next penny.Hint: Find
 before you plug numbers into your calculator!
before you plug numbers into your calculator! 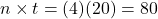
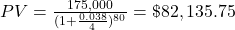
$82,135.75
Try It 6.45
-
The money invested in an account bearing an annual interest rate of
 (in decimal form), compounded
(in decimal form), compounded 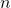 times per year for
times per year for 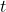 years, is called the present value,
years, is called the present value, 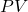 , of the account (or of the money) and found using the formula
, of the account (or of the money) and found using the formula 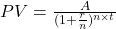 where
where  is the value of the account at the investment’s end. Always round this value up to the next penny.
is the value of the account at the investment’s end. Always round this value up to the next penny.It is 35 years until Hajun turns 65.
Hint: Find
 before you plug numbers into your calculator!
before you plug numbers into your calculator! 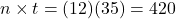
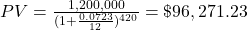
Hajun needs to invest $96,271.23.
$96,271.23
Try It 6.46
-
Effective annual yield is
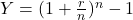 where
where 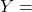 effective annual yield,
effective annual yield, 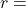 the interest rate in decimal form, and
the interest rate in decimal form, and 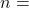 the number of times the interest is compounded in a year.
the number of times the interest is compounded in a year. 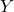 is interpreted as the equivalent annual simple interest rate.
is interpreted as the equivalent annual simple interest rate.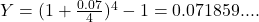
Effective annual yield: 7.19%
Earning 7% compounded quarterly gives you an effective annual yield of 7.19%, which is the equivalent of the annual simple interest rate.
A rate of 7% compounded quarterly is equivalent to a simple interest rate of 7.19%.
Try It 6.47
-
Effective annual yield is
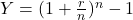 where
where 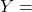 effective annual yield,
effective annual yield, 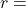 the interest rate in decimal form, and
the interest rate in decimal form, and 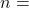 the number of times the interest is compounded in a year.
the number of times the interest is compounded in a year. 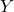 is interpreted as the equivalent annual simple interest rate.
is interpreted as the equivalent annual simple interest rate.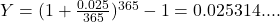
Effective annual yield: 2.53%
Earning 2.5% compounded daily gives you an effective annual yield of 2.53%, which is the equivalent of the annual simple interest rate.
The effective annual yield is 2.53%.
Try It 6.48
-
Find the effective annual yield of each bank.
Smith Bank 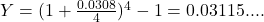
Effective annual yield: 3.11%Park Bank 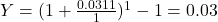
Effective annual yield: 3%Town Bank 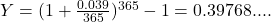
Effective annual yield: 3.98%Community Bank 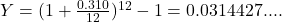
Effective annual yield: 3.14%Community Bank has the highest effective annual yield at 3.14%.
The effective annual yields for the banks are 3.1158% for Smith Bank, 3.11% for Park Bank, 3.1381% for Town Bank, and 3.144% for Community Bank. Community Bank has the best yield.
Try It 6.49
-
Income Amount Expense Amount Electrician $3,375.00 Mortgage $987.00 Side jobs $300.00 Truck payment $589.00 Truck insurance $312.00 Utilities $167.00 Clothing $150.00 Entertainment $400.00 Credit card $325.00 Food $470.00 Gasoline $375.00 Total $3,675.00 Total $3,775.00 Add the income amounts:
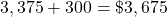
Add the expenses:
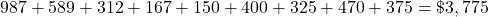
The expenses are greater than the income by $100.
Mateo’s budget is below.
Income Source Amount Expense Amount Electrician $3,375.00 Mortgage $987 Side jobs $300.00 Truck payment $589 Truck insurance $312 Utilities $167 Clothing $150 Entertainment $400 Credit Card $325 Food $470 Gasoline $375 His total monthly income is $3,675.00, and his monthly expenses are $3,775. Mateo falls $100.00 short each month.
Try It 6.50
-
Income Amount Expense Amount Engineer $6,093.75 Mortgage $1,452.89 Car payment $627.38 Car insurance $179.00 Health insurance $265.00 Utilities $320.00 Clothing $150.00 Entertainment $400.00 Credit card $450.00 Food $370.00 Gasoline $175.00 Total $6,093.75 Total $4,389.27 The income amount is $6,093.75.
Add the expenses:
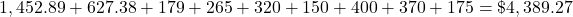
The income is greater than the expenses by $1,704.48.
Maddy’s budget is below.
Income Source Amount Expense Amount Engineer $6,093.75 Mortgage $1,452.89 Car payment $627.38 Car insurance $179.00 Health Insurance $265.00 Utilities $320.00 Clothing $150.00 Entertainment $400.00 Credit Card $450.00 Food $370.00 Gasoline $175.00 Her total monthly income is $6,093.75, and her monthly expenses are $4,389.27. Maddy has $1,704.48 in extra income per month. This is her cushion in the budget.
Try It 6.51
-
Her new budget:
Income Amount Expense Amount Nursing $3,765.40 Mortgage $1,240.00 Part-time $672.00 Car payment $489.00 Student loan $728.00 Car insurance $139.00 Utilities $295.00 Clothing $150.00 Entertainment $300.00 Credit card $200.00 Food $400.00 Gasoline $250.00 Total $4,437.40 Total $4,191.00 New income – expenses = $246.40 with the mortgage and increase in utilities.
She still has an excess in her budget.
She would change from a rent of $1,050 to a mortgage of $1,240.
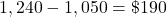 This is an increase of $190.
This is an increase of $190.Her utilities would also change from $130 to $295.
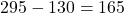 This is an increase of $165.
This is an increase of $165.This is an overall increase of
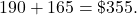
Her budget in the example had an excess of $601.40 as a cushion. Her cushion can cover this $355 increase in expenses.
Heather’s budget is now
Income Source Amount Expense Amount Nursing $3,765.40 Mortgage $1,240 Part-time $672.00 Car Payment $489 Student Loan $728 Car Insurance $139 Utilities $295 Clothing $150 Entertainment $300 Credit Card $200 Food $400 Gasoline $250 The changes have added $355.00 to her budget. As her extra income is $601.40, she can afford the changes.
Try It 6.52
-
Income Amount Expense Amount Nursing $3,765.40 Rent $1,050.00 Part-time $672.00 Car payment $489.00 Student loan $728.00 Car insurance $139.00 Utilities $130.00 Clothing $150.00 Entertainment $300.00 Credit card $200.00 Food $400.00 Gasoline $250.00 Total $4,437.40 Total $3,836.00 Income – expenses = $601.40
The 50-30-20 principle suggests spending 50 percent of your budget on necessary expenses (basic living requirements and debt services such as mortgage/rent, utilities, car, insurance, health care, groceries, gasoline, child care, and minimum debt payments), 30 percent of your budget for wants (restaurants, vacations, hobby costs), and 20 percent should be set aside (retirement funds, stocks, an emergency fund should have at least 3 months of income, other investments).
Heather’s monthly income is $4,437.40.
50% Needs 30% Wants 20% Set Aside Goal $2,218.70 $1,331.22 $887.48 Actual Rent: $1,050
Car payment: $489
Student loan: $728
Car insurance: $139
Utilities: $130
Clothing: $150
Credit card: $200
Food: $400
Gasoline: $250
Total: $3536
This is above what she should have in this category.Entertainment: $300
Total: $300
This is below what she should have in this category, but it is possible that what she charged on the credit card and clothing could be moved over to this column if you knew what it was.Unused: $601.40 Heather’s total income is $4,437.40.
For the necessities, Heather should budget $2,218.70.
For her wants, she should budget $1,331.22.
For savings and extra debt service, she should budget $887.48.
Her necessities total $3,536.00, which exceeds the suggested budget amount of $2,218.70.
Her wants total $300.00, which is below the suggested budget amount of $1,331.22.
Her excess income is $601.40, which is below the suggested budget amount of $887.48.
Heather should make some changes.
Try It 6.53
-
The 50-30-20 principle suggests spending 50 percent of your budget on necessary expenses (basic living requirements and debt services such as mortgage/rent, utilities, car, insurance, health care, groceries, gasoline, child care, and minimum debt payments), 30 percent of your budget for wants (restaurants, vacations, hobby costs), and 20 percent should be set aside (retirement funds, stocks, an emergency fund should have at least 3 months of income, other investments).
The monthly income: $3,263.44.
Spend 50 percent on needs. Fifty percent is $1,631.72.
Spend 30 percent on wants. Thirty percent is $979.03.
Set aside 20 percent in savings, investments, and debt service. Twenty percent is $652.69.
Keeping within or below his budget can build his savings.
Elijah should budget $1,631.72 for needs, $979.03 for wants, and $652.69 for savings and debt service. When choosing where to live, what to eat, and what to drive, he should make choices that keep those costs, combined with debt service costs, gasoline, and utilities, below $1,631.72. This means he will have to make decisions about what his priorities are. Elijah should then figure out his wants, and stay within the limits here, that is, keep those costs below $979.03. Finally, he can begin to build his savings with the remaining $652.69.
Try It 6.54
-
The 50-30-20 principle suggests spending 50 percent of your budget on necessary expenses (basic living requirements and debt services such as mortgage/rent, utilities, car, insurance, health care, groceries, gasoline, child care, and minimum debt payments), 30 percent of your budget for wants (restaurants, vacations, hobby costs), and 20 percent should be set aside (retirement funds, stocks, an emergency fund should have at least 3 months of income, other investments).
Monthly income = $43,700 / 12
The monthly income: $3,641.66.
Spend 50 percent on needs. Fifty percent is $1,820.83.
Spend 30 percent on wants. Thirty percent is $1,092.50.
Set aside 20 percent in savings, investments, and debt service. Twenty percent is $728.33.
Her monthly income is $3,641.66.
Needs (50%): $1,820.83, Wants (30%): $1,092.50, Savings (20%): $728.33 -
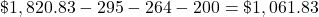
$1,061.83
-
Spend 30 percent on wants. Thirty percent is $1,092.50.
Set aside 20 percent in savings, investments, and debt service. Twenty percent is $728.33.
$1,092.50, $728.33
-
She only has budgeted $1,061.83 for other necessities. It is difficult to imagine Fran being able to afford to change jobs and move, unless she reallocates money that she would want to save or use for entertainment or takes on another job. If Fran uses all the money that the 50-30-20 budget sets aside for savings, she then would have $1,790.16 to spend on those other necessities. If she moves away from the 50-30-20 philosophy, she may be able to afford the move. However, that means changing her priorities.
Try It 6.55
-
The amount in the account, A, when the principal, P, is invested at an annual interest rate of r (in decimal form), compounded n times per year for t years is found using the formula
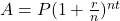 .
.It will help you get the right answer from your calculator to find nt separately.
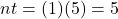
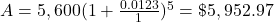
$5,952.97
Try It 6.56
-
The amount in the account, A, when the principal, P, is invested at an annual interest rate of r (in decimal form), compounded n times per year for t years is found using the formula
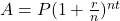 .
.It will help you get the right answer from your calculator to find nt separately.
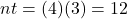
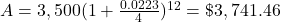
$3,741.46
Try It 6.57
-
The amount in the account, A, when the principal, P, is invested at an annual interest rate of r (in decimal form), compounded n times per year for t years is found using the formula
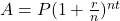 .
.It will help you get the right answer from your calculator to find nt separately.
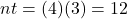
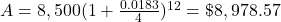
$8,978.57
Try It 6.58
-
The return on investment (ROI) is the percent difference between the initial investment (P) and the final value of the investment (FV), or
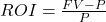 , expressed as a percentage. The length of time of the investment is not considered in ROI.
, expressed as a percentage. The length of time of the investment is not considered in ROI.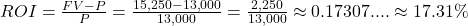
17.31%
-
The return on investment (ROI) is the percent difference between the initial investment (P) and the final value of the investment (FV), or
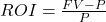 , expressed as a percentage. The length of time of the investment is not considered in ROI.
, expressed as a percentage. The length of time of the investment is not considered in ROI.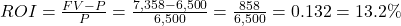
13.2%
Try It 6.59
-
$42,499.63
The future value of an ordinary annuity is
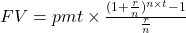 , where FV is the future value of the annuity, pmt is the payment, r is the annual interest rate (in decimal form), n is the number of compounding periods per year, and t is the number of years. It is important to note that the number of deposits per year and the number of compounding periods per year must be the same.
, where FV is the future value of the annuity, pmt is the payment, r is the annual interest rate (in decimal form), n is the number of compounding periods per year, and t is the number of years. It is important to note that the number of deposits per year and the number of compounding periods per year must be the same.It will help you get the right answer using your calculator to find
 first.
first.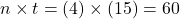
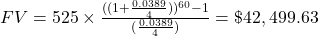
The extra parentheses were added to help you enter the expression properly in your calculator.
Try It 6.60
-
The future value of an ordinary annuity is
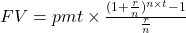 , where FV is the future value of the annuity, pmt is the payment, r is the annual interest rate (in decimal form), n is the number of compounding periods per year, and t is the number of years. It is important to note that the number of deposits per year and the number of compounding periods per year must be the same.
, where FV is the future value of the annuity, pmt is the payment, r is the annual interest rate (in decimal form), n is the number of compounding periods per year, and t is the number of years. It is important to note that the number of deposits per year and the number of compounding periods per year must be the same.It will help you get the right answer using your calculator to find
 first.
first.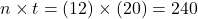
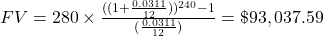
$93,037.59
Try It 6.61
-
$1,227.30
To compute the payment to reach a final goal, the payment (pmt) of an ordinary annuity to reach a specific future value (FV) is
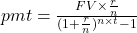 , where r is the annual interest rate (in decimal form), n is the number of compounding periods per year, and t is the number of years. Round up!
, where r is the annual interest rate (in decimal form), n is the number of compounding periods per year, and t is the number of years. Round up!Once again, it will help you get the right answer using your calculator to find
 first.
first.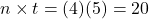
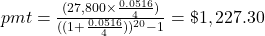
Additional parentheses were added to help you enter the expression properly in your calculator.
Try It 6.62
-
Use your knowledge of percents. Remember to convert the percentage to a decimal.
3.1% of 500

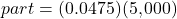 [latex]= \$237.50[/latex]
[latex]= \$237.50[/latex]Maureen receives $237.50 per year.
On the maturity date, she receives the interest and the initial payment.
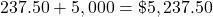
$237.50 per year, $5,237.50 on maturity date.
Try It 6.63
-
Use the formula for the future value of an investment, A, when the principal, P, is invested at an annual interest rate of r (in decimal form), compounded n times per year for t years:
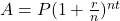 .
.Hint: Find nt before you plug numbers into your calculator!
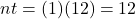
It will help you get the right results. Use those parentheses in your calculator, too!
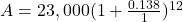
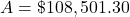
Rixie expects the stock to be worth $108,501.30.
$108,501.30
Try It 6.64
-
The percent yield for a stock, Yld%, is
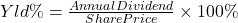 .
.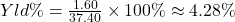
4.28%
-
The percent yield for a stock, Yld%, is
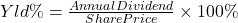 .
.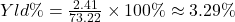
3.29%
Try It 6.65
-
Look for the “Open” label to find the current price of $30.68.
Looking at the table, the current price of a share is $30.68.
-
Look for the “52 Week Range” label, which tells you the 52-week high of $56.28 and the 52-week low of $30.25.
The high was $56.28, and the low was $30.05.
-
Look for the “Ex-Dividend Date” label, which tells you when the dividend is expected: August 4, 2022.
August 4, 2022
-
Look for “Yield” on the display, which tells you the yield is 4.77%.
4.77%
-
Look for the “EPS” label, which tells you the earnings per share is $4.66.
$4.66
Try It 6.66
-
$336.00
Each share pays $1.12.
Because the number of shares is 300, multiply 300 by $1.12.
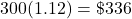
Yulia earns $336.
Try It 6.67
-
Ginny bought 200 shares of stock at $9.76 per share:
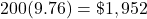 .
.Later, 200 shares sold for $10.02 per share:
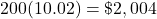 .
.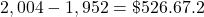
$52
-
The return on investment (ROI) is the percent difference between the initial investment (P) and the final value of the investment (FV), or
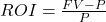 , expressed as a percentage. The length of time of the investment is not considered in ROI.
, expressed as a percentage. The length of time of the investment is not considered in ROI.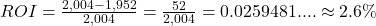
2.6%
Try It 6.68
-
The future value is
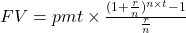 , where FV is the future value, pmt is the payment, r is the annual interest rate (in decimal form), n is the number of compounding periods per year, and t is the number of years. It is important to note that the number of deposits per year and the number of compounding periods per year must be the same.
, where FV is the future value, pmt is the payment, r is the annual interest rate (in decimal form), n is the number of compounding periods per year, and t is the number of years. It is important to note that the number of deposits per year and the number of compounding periods per year must be the same.It will help you get the right answer using your calculator to find
 first.
first.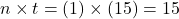
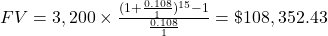
The extra parentheses were added to help you enter the expression properly in your calculator.
$108,352.43
Try It 6.69
-
$1,815.83
To compute the payment to reach a final goal, the payment (pmt) of an ordinary annuity or mutual fund to reach a specific future value (FV) is
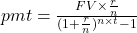 , where r is the annual interest rate (in decimal form), n is the number of compounding periods per year, and t is the number of years. Round up!
, where r is the annual interest rate (in decimal form), n is the number of compounding periods per year, and t is the number of years. Round up!Once again, it will help you get the right answer using your calculator to find
 first.
first.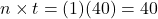
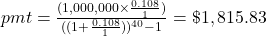
Additional parentheses were added to help you enter the expression properly in your calculator.
Try It 6.70
-
23.75%
Each year, Maureen was paid 4.75% of the $5,000 she invested.

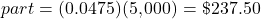
Maureen is paid interest each year for five years.
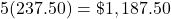
The return on investment (ROI) is the percent difference between the initial investment (P) and the final value of the investment (FV), or
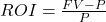 , expressed as a percentage. The length of time of the investment is not considered in ROI.
, expressed as a percentage. The length of time of the investment is not considered in ROI.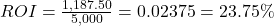
Try It 6.71
-
Maureen’s FV is the $5,000 she invested plus the $1,187.50 she earned for a total of $6,187.50. Her principal was $5,000. The time is 5 years.
The annual return
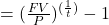 , where t is the number of years, FV is the new value, and P is the starting principal. Convert the answer to a percent.
, where t is the number of years, FV is the new value, and P is the starting principal. Convert the answer to a percent.annual return
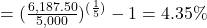
Maureen’s annual return on investment is 4.35 percent.
4.35%
Try It 6.72
-
The return on investment (ROI) is the percent difference between the initial investment (P) and the final value of the investment (FV), or
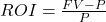 , expressed as a percentage. The length of time of the investment is not considered in ROI.
, expressed as a percentage. The length of time of the investment is not considered in ROI.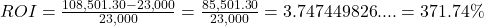
Rixie’s ROI is 371.74 percent.6.72.2
371.74%
-
The annual return
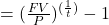 , where t is the number of years, FV is the new value, and P is the starting principal. Convert the answer to a percent.
, where t is the number of years, FV is the new value, and P is the starting principal. Convert the answer to a percent.annual return
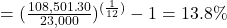
The annual return was 13.8 percent.
13.8%
Try It 6.73
-
$3,336.13
To compute the payment to reach a final goal for an annuity or mutual fund, the payment (pmt) is
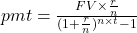 , where r is the annual interest rate (in decimal form), n is the number of compounding periods per year, and t is the number of years. Round up!
, where r is the annual interest rate (in decimal form), n is the number of compounding periods per year, and t is the number of years. Round up!Once again, it will help you get the right answer using your calculator to find
 first.
first.
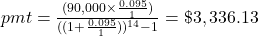
Additional parentheses were added to help you enter the expression properly in your calculator.
Pete and Erin need to set aside $3,336.13 each year.
Try It 6.74
-
Traditional
Try It 6.75
-
An employer will match up to 7.5% of any employee’s salary.
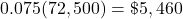
The amount Jamie can deposit that will be matched by the employer is $5,460.
$5,460
-
The amount Jamie deposits plus the employer’s match:
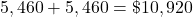 .
.The total is $10,920.
$10,920
-
Jamie deposits $5,460. The account ends up with $10,920.
The return on investment (ROI) is the percent difference between the initial investment (P) and the final value of the investment (FV), or
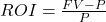 , expressed as a percentage. The length of time of the investment is not considered in ROI.
, expressed as a percentage. The length of time of the investment is not considered in ROI.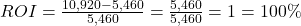
The ROI is 100%.
100% return on the $5,460 deposit
Try It 6.76
-
$813,128.60
The future value of an ordinary annuity or mutual fund is
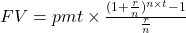 , where FV is the future value of the annuity, pmt is the payment, r is the annual interest rate (in decimal form), n is the number of compounding periods per year, and t is the number of years. It is important to note that the number of deposits per year and the number of compounding periods per year must be the same.
, where FV is the future value of the annuity, pmt is the payment, r is the annual interest rate (in decimal form), n is the number of compounding periods per year, and t is the number of years. It is important to note that the number of deposits per year and the number of compounding periods per year must be the same.It will help you get the right answer using your calculator to find
 first.
first.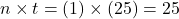
The combined monthly payment is
 .
.It is only compounded annually, so for the payment, multiply the monthly payment by 12.
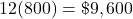
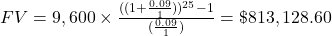
The extra parentheses were added to help you enter the expression properly in your calculator.
Crystal’s account will be worth $813,128.60.
-
$457,384.83
It is only compounded annually, so for the payment, multiply the monthly payment by 12.
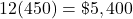
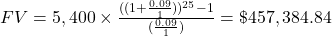
Without matching funds, her account will be worth $457,384.84.
Try It 6.77
-
The amount of interest, I, to be paid for one period of a loan with remaining principal, P, is
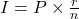 , where r is the interest rate in decimal form and n is the number of payments in a year. Because r is the interest rate in a year, t is 1 and does not impact the calculation. Note, interest paid to lenders is always rounded up to the nearest penny.
, where r is the interest rate in decimal form and n is the number of payments in a year. Because r is the interest rate in a year, t is 1 and does not impact the calculation. Note, interest paid to lenders is always rounded up to the nearest penny.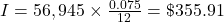
$355.91
-
The amount of interest, I, to be paid for one period of a loan with remaining principal, P, is
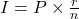 , where r is the interest rate in decimal form and n is the number of payments in a year. Because r is the interest rate in a year, t is 1 and does not impact the calculation. Note, interest paid to lenders is always rounded up to the nearest penny.
, where r is the interest rate in decimal form and n is the number of payments in a year. Because r is the interest rate in a year, t is 1 and does not impact the calculation. Note, interest paid to lenders is always rounded up to the nearest penny.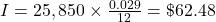
$62.48
Try It 6.78
-
To compute the payment to pay down a loan with beginning principal, P, the payment (pmt) is
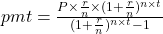 , where r is the annual interest rate (in decimal form), n is the number of compounding periods per year, and t is the number of years. Note, payment to lenders is always rounded up to the next penny.
, where r is the annual interest rate (in decimal form), n is the number of compounding periods per year, and t is the number of years. Note, payment to lenders is always rounded up to the next penny.Once again, it will help you get the right answer from your calculator to find
 first.
first.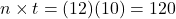
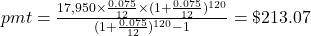
Additional parentheses were added to help you enter the expression properly in your calculator.
The payment is $213.07.
$213.07
-
To compute the payment to pay down a loan with beginning principal, P, the payment (pmt) is
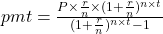 , where r is the annual interest rate (in decimal form), n is the number of compounding periods per year, and t is the number of years. Note, payment to lenders is always rounded up to the next penny.
, where r is the annual interest rate (in decimal form), n is the number of compounding periods per year, and t is the number of years. Note, payment to lenders is always rounded up to the next penny.Once again, it will help you get the right answer from your calculator to find
 first.
first.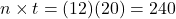
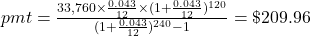
Additional parentheses were added to help you enter the expression properly in your calculator.
The payment is $209.96.
$209.96
Try It 6.79
-
Look at the top row. The label to the left says “Loan Amount.” To the right, you see the loan amount, $34,700. This is usually called the principal in the formulas.
Look for the label called “Interest Rate (annual)” in the second row. Beside it, you see the interest rate of 3.79%.
Look for the label in the third row called “Term (Years).” Beside it, you see the number of years for the loan, which is 6 years.
$34,700, 3.79%, 6 years
-
In the seventh row, second column, you see the header title, “Payment.” Beginning in the ninth row, second column, you see the monthly payment of $539.57.
$539.57
-
In the seventh row, first column, you see the header title, “Month.” In the last column on the right, you see the header title, “Balance.”
Scroll down in the first column to find Month 20. While in that row, look across to the last column in that row to find the balance is $25,837.42.
$25,837.42
-
In the seventh row, second column, you see the header title, “Month.” In the fourth column of that row, you see the header title, “Interest.”
Look down the first column for Month 5. While in that row, look across to the fourth column of that row to see that the interest for Month 5 is $104.14.
$104.14
-
In the seventh row, second column, you see the header title, “Month.” In the fifth column of that row, you see the header title, “Total Interest.”
Look down the first column for Month 24. While in that row, look across to the fifth column of that row to see that the total interest for Month 24 is $2,246.62.
$2,246.62
-
The amount paid to principal increases each month
Try It 6.80
-
The cost of finance is the sum of the interest and any fees paid for the loan. Add that to the interest.
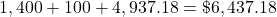
$6,437.18
Try It 6.81
-
The costs are $34,845.
The awards are
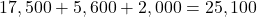 .
.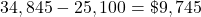
The funding gap is $9,745.
$9,745
Try It 6.82
-
The debt so far:
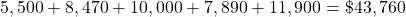
Tiana is an independent student, so for the first year, she can borrow $9,500. For the second year, she can borrow $10,500. For additional years, she can borrow $12,500.
The total maximum for undergraduates is $57,500.
How much can she still borrow?
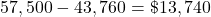 .
.Tiana still is $13,740 away from the total allowed maximum, so she can borrow the yearly maximum of $12,500 in her sixth year.
Tiana can take out $12,500, the maximum in year 6.
Try It 6.83
-
The costs are $39,200 for the third year.
The awards are
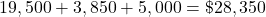 .
.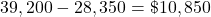
The funding gap is $10,850.
Assuming that Makenzy is a dependent student, the loan limit for a third-year student is $7,500 (but no more than $5,500 in subsidized loans).
After the maximum amount of loans, find the remaining amount to be funded.
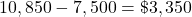
Makenzy needs to come up with another $3,350 to fund her education.
Gap = $10,850, Federal loans = $7,500, Remaining $3,350
Try It 6.84
-
The amount due for a loan, A, when the principal, P, an interest rate of r (in decimal form), compounded n times per year for t years is found using the formula
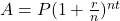 .
.Hint: Find nt before you plug numbers into your calculator! It will help you get the right results.
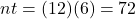 if paid the full six years.
if paid the full six years.But they are asking for the balance in May when starting in August, so subtract three payments.

Use those parentheses in your calculator, too!
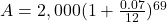
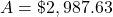
$2,987.63
Try It 6.85
-
$82.70
The standard plan is 12 payments a year for 10 years.
To compute the payment to pay down a loan with beginning principal, P, the payment (pmt) is
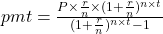 , where r is the annual interest rate (in decimal form), n is the number of compounding periods per year, and t is the number of years. Note, payment to lenders is always rounded up to the next penny.
, where r is the annual interest rate (in decimal form), n is the number of compounding periods per year, and t is the number of years. Note, payment to lenders is always rounded up to the next penny.If the number of periods per year is 1, then the formula is simplified to
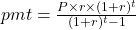 .
.Once again, it will help you get the right answer from your calculator to find
 first.
first.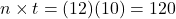
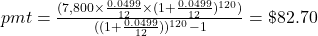
Additional parentheses were added to help you enter the expression properly in your calculator.
-
$137.42
The standard plan is 12 payments a year for 10 years.
To compute the payment to pay down a loan with beginning principal, P, the payment (pmt) is
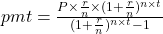 , where r is the annual interest rate (in decimal form), n is the number of compounding periods per year, and t is the number of years. Note, payment to lenders is always rounded up to the next penny.
, where r is the annual interest rate (in decimal form), n is the number of compounding periods per year, and t is the number of years. Note, payment to lenders is always rounded up to the next penny.If the number of periods per year is 1, then the formula is simplified to
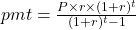 .
.Once again, it will help you get the right answer from your calculator to find
 first.
first.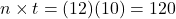
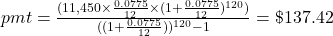
Additional parentheses were added to help you enter the expression properly in your calculator.
Try It 6.86
-
The standard plan is 12 payments a year for 10 years.
To compute the payment to pay down a loan with beginning principal, P, the payment (pmt) is
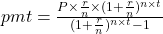 , where r is the annual interest rate (in decimal form), n is the number of compounding periods per year, and t is the number of years. Note, payment to lenders is always rounded up to the next penny.
, where r is the annual interest rate (in decimal form), n is the number of compounding periods per year, and t is the number of years. Note, payment to lenders is always rounded up to the next penny.If the number of periods per year is 1, then the formula is simplified to
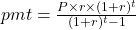 .
.Once again, it will help you get the right answer from your calculator to find
 first.
first.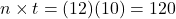
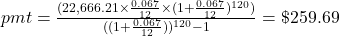
Additional parentheses were added to help you enter the expression properly in your calculator.
$259.69
Try It 6.87
-
There is no impact on Ryann’s interest rate. The total Ryann pays back increases since the interest is extended to more periods.
Try It 6.88
-
The standard plan is 12 payments a year for 10 years.
To compute the payment to pay down a loan with beginning principal, P, the payment (pmt) is
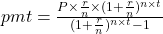 , where r is the annual interest rate (in decimal form), n is the number of compounding periods per year, and t is the number of years. Note, payment to lenders is always rounded up to the next penny.
, where r is the annual interest rate (in decimal form), n is the number of compounding periods per year, and t is the number of years. Note, payment to lenders is always rounded up to the next penny.If the number of periods per year is 1, then the formula is simplified to
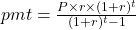 .
.Once again, it will help you get the right answer from your calculator to find
 first.
first.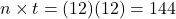
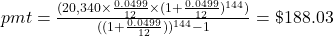
Additional parentheses were added to help you enter the expression properly in your calculator.
$188.03
Try It 6.89
-
150 percent of the poverty guideline is:
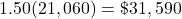 .
.Discretionary income is the amount Jamie earns over $31,590.
Subtract $31,590 from Jamie’s income of $36,900 to find her discretionary income.
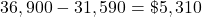
Jamie’s discretionary income is $5,310.
$5,310
Try It 6.90
-
REPAYE plans have payment amounts that are 10% of discretionary income.
Discretionary income is the excess of 150% of the poverty guideline.
Find 150 percent of $18,310: 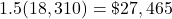 .
.Discretionary income is the excess over $27,465: 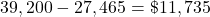 .
.Lauren’s discretionary income is $11,735.
$11,735
-
Ten percent of her discretionary income of $11,735 is: 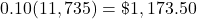 .
.Divide by 12 to find the monthly payment: 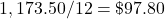 .
.Lauren’s monthly payment is $97.80.
$97.80
Try It 6.91
-
Store-issued credit cards
-
Fees (both annual and penalty fees), reward programs, credit limits
-
Travel and entertainment cards
Try It 6.92
-
Look at the upper-right corner of the statement for the label “Statement Period.” Underneath the label, you will see the start date of the period after “From” and the end date of the period after “To.”
From April 01, 2015
To April 30, 2015
April 01 2015 to April 30 2015
-
Almost halfway down in the left column is a bold label, “Your New Balance.” Just below that label is a smaller label, “Credit Limit.” Beside that label, you see $9000.00.
$9,000.00
-
Just above the “Your New Balance” label is the label “Subtotal.”
Above the “Subtotal” label is the label “Fees.” The fees are $5.99.
$5.99
Try It 6.93
-
Use a list of transactions.
Step 1: Create a table that has the sum of transactions for each day. Expenditures are positive. Payments are negative.
Step 2: Add a column, “Days Until Balance Changed,” where you write the number of days until the balance changed. This is the difference between the date of this row and the next.
Step 3: Add a column, “Balance Times Days,” where you multiply the previous two columns.
Step 4: Sum the last column.
Step 5: Divide the sum by the number of days in the month. This is the average daily balance.
Date Activity Transaction Balance Days Until Balance Changed Balance Times Days 1-Jun Balance 563.8 563.8 1 563.8 2-Jun Gas-Groceries 110.92 674.72 13 8771.36 15-Jun Movie-payment –211.25 463.47 12 5561.64 27-Jun Pharmacy 31.21 494.68 1 494.68 28-Jun Gas 48 542.68 3 1628.04 The average daily balance is the sum of the last column divided by the number of days in the month.
The average daily balance =
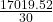 is approximately $567.32.
is approximately $567.32.$567.32
Try It 6.94
-
The interest charge, I, for a credit card during a billing cycle is
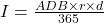 , where ADB is the average daily balance, r is the annual percentage rate as a decimal, and d is the number of days in the billing cycle. As before, interest is rounded up to the next penny.
, where ADB is the average daily balance, r is the annual percentage rate as a decimal, and d is the number of days in the billing cycle. As before, interest is rounded up to the next penny.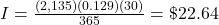
$22.64
-
The interest charge, I, for a credit card during a billing cycle is
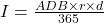 , where ADB is the average daily balance, r is the annual percentage rate as a decimal, and d is the number of days in the billing cycle. As before, interest is rounded up to the next penny.
, where ADB is the average daily balance, r is the annual percentage rate as a decimal, and d is the number of days in the billing cycle. As before, interest is rounded up to the next penny.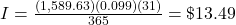
$13.49
-
The interest charge, I, for a credit card during a billing cycle is
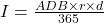 , where ADB is the average daily balance, r is the annual percentage rate as a decimal, and d is the number of days in the billing cycle. As before, interest is rounded up to the next penny.
, where ADB is the average daily balance, r is the annual percentage rate as a decimal, and d is the number of days in the billing cycle. As before, interest is rounded up to the next penny.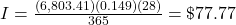
$77.77
Try It 6.95
-
Add the balance before interest and the new interest:
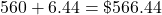 .
.$566.44
-
Add the balance before interest and the new interest:
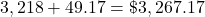 .
.$3,267.17
Try It 6.96
-
$1,152.35
Find the average daily balance.
Use a list of transactions.
Step 1: Create a table that has the sum of transactions for each day. Expenditures are positive. Payments are negative.
Step 2: Add a column, “Days Until Balance Changed,” where you write the number of days until the balance changed. This is the difference between the date of this row and the next.
Step 3: Add a column, “Balance Times Days,” where you multiply the previous two columns.
Date Activity Transaction Balance Days Until Balance Changed Balance Times Days 1-Aug Balance $982.45 $982.45 4 $3,929.80 5-Aug Food $125.31 $1,107.76 8 $8,862.08 13-Aug Payment –$500.00 $607.76 1 $607.76 14-Aug Gas/Pizza/Shoes $178.09 $785.85 5 $3,929.25 19-Aug Electric Bill $178.34 $964.19 2 $1,928.38 21-Aug Internet/Food $130.44 $1,094.63 9 $9,851.67 30-Aug Gasoline $43.18 $1,137.81 2 $1,137.81 Step 4: Sum the last column.
$31,384.56
Step 5: Divide the sum by the number of days in the month. This is the average daily balance.
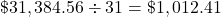
The average daily balance (ADB) is $1,012.41.
The interest charge, I, for a credit card during a billing cycle is
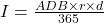 , where ADB is the average daily balance, r is the annual percentage rate as a decimal, and d is the number of days in the billing cycle. As before, interest is rounded up to the next penny.
, where ADB is the average daily balance, r is the annual percentage rate as a decimal, and d is the number of days in the billing cycle. As before, interest is rounded up to the next penny.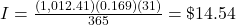
Add the interest to the last balance in the table.
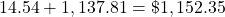
Try It 6.97
-
For this amount, use 1 percent plus interest plus fees. There are no fees.
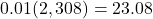
One percent plus interest is:
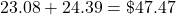 .
.$47.47
-
For this amount, use $25 interest plus fees.
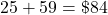
$84.00
-
For this amount, use the balance plus fees. There are no fees.
$19.90
Try It 6.98
-
Add 8% and 2.1% for a total percentage of 10.1%.
Find 10.1% of $28,975.
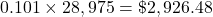
Add this to the cost and fees.
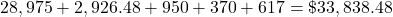
$33,838.48
Try It 6.99
-
Find 6.5% of $36,250.
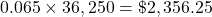
Add this to the cost and fees.
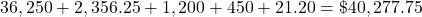
The car’s total cost is 40,277.75.
Subtract the $7,500 down payment to get $32,777.75.
$32,777.75
Try It 6.100
-
To compute the payment to pay down a loan with beginning principal, P, the payment (pmt) is
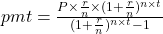 , where r is the annual interest rate (in decimal form), n is the number of compounding periods per year, and t is the number of years. Note, payment to lenders is always rounded up to the next penny.
, where r is the annual interest rate (in decimal form), n is the number of compounding periods per year, and t is the number of years. Note, payment to lenders is always rounded up to the next penny.Once again, it will help you get the right answer from your calculator to find
 first.
first.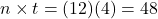
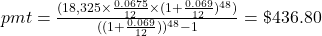
Additional parentheses were added to help you enter the expression properly in your calculator.
$436.70
-
To compute the payment to pay down a loan with beginning principal, P, the payment (pmt) is
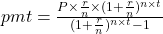 , where r is the annual interest rate (in decimal form), n is the number of compounding periods per year, and t is the number of years. Note, payment to lenders is always rounded up to the next penny.
, where r is the annual interest rate (in decimal form), n is the number of compounding periods per year, and t is the number of years. Note, payment to lenders is always rounded up to the next penny.Once again, it will help you get the right answer from your calculator to find
 first.
first.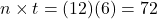
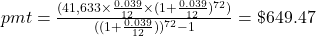
Additional parentheses were added to help you enter the expression properly in your calculator.
$649.47
Try It 6.101
-
$1,516.05
Try It 6.102
-
Add the values together.
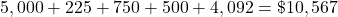
$10,567.00
Try It 6.103
-
The monthly depreciation for a car, MD, is
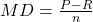 , where P is the price paid for the car, R is the residual value of the car, and n is the number of months of the lease.
, where P is the price paid for the car, R is the residual value of the car, and n is the number of months of the lease.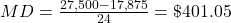
$401.05
Try It 6.104
-
6.25%
-
The money factor (MF) is
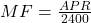 , where APR is the annual percentage rate as a decimal.
, where APR is the annual percentage rate as a decimal.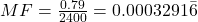
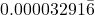
Try It 6.105
-
$74.49
-
You need to find the money factor first.
The money factor (MF) is
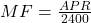 , where APR is the annual percentage rate as a decimal.
, where APR is the annual percentage rate as a decimal.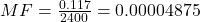
The payment, PMT, for a lease is
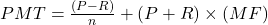 , where P is the price paid for the car, R is the residual value of the car after the n months of the lease, and MF is the money factor of the lease.
, where P is the price paid for the car, R is the residual value of the car after the n months of the lease, and MF is the money factor of the lease.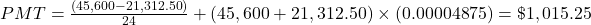
$1,015.25
Try It 6.106
-
Purchase
-
Purchase
Try It 6.107
-
Personal injury protection
-
Liability insurance
Try It 6.108
-
Divide the $2,190 cost per year by 12 to get $182.50.
Add that to the monthly car payment of $410.86 to get the total monthly cost of $593.36.
$593.36
Try It 6.109
-
Item Cost Calculations Yearly cost New tires every five years $390 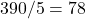
78 Oil changes every three months $59.99 Every three months is four times a year. 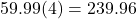
239.96 Inspections once a year $25 25 Wipers once a year $115 115 Air filter once a year $46.25 46.25 Yearly Total: 504.21 Divide the yearly total to find the monthly total is $42.02.
Natalie needs $42.02 to cover these costs.
$42.02
Try It 6.110
-
To compute the payment to pay down a loan with beginning principal, P, the payment (pmt) is
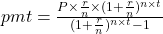 , where r is the annual interest rate (in decimal form), n is the number of compounding periods per year, and t is the number of years. Note, payment to lenders is always rounded up to the next penny.
, where r is the annual interest rate (in decimal form), n is the number of compounding periods per year, and t is the number of years. Note, payment to lenders is always rounded up to the next penny.Once again, it will help you get the right answer from your calculator to find
 first.
first.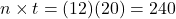
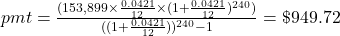
Additional parentheses were added to help you enter the expression properly in your calculator.
$949.72
Try It 6.111
-
In the previous exercise, you found the monthly payment was $949.72.
The total paid, T, on a t year mortgage with monthly payments pmt is
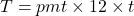 .
.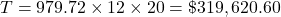
Arthur pays $319,620.60 in total.
$319,620.60
Try It 6.112
-
From the previous exercise, you know Arthur pays $319,620.60 in total. Subtract the original cost of $225,879 to find the cost of financing was $93,741.60.
$93,741.60
Try It 6.113
-
Look at the second row of the table to find the label “Interest Rate (annual).” Beside it, you will see the interest rate is 6.10%.
6.1%
-
Look at the fifth row of the table to find the label “Monthly Payment.” To the right, you will see the monthly payment is $1,383.61.
$1,383.61
-
Look at the seventh row. The first column has the label “Month” and the third column has the label “Principal.” Go down to the row that shows Month 235. You will see that the third column in that row shows you the principal for that month is $730.38.
$730.38
-
Look at the seventh row. The first column has the label “Month” and the fourth column has the label “Interest.” Go down to the row that shows Month 215. You will see that the fourth column in that row shows you the interest for that month is $723.66.
$723.66
-
Look at the seventh row. The first column has the label “Month” and the last column has the label “Balance.” Go down to the row that shows Month 227. You will see that the last column in that row shows you the remaining balance for that month is $133,513.05.
$133,513.05
-
Look at the seventh row. The first column has the label “Month,” the third column has the label “Principal,” and the fourth column has the label “Interest.” Go down the table and look for the first row where the principal is greater than the interest. That happens in the row for Month 225.
Payment 225
Try It 6.114
-
Find her payment using the loan formula. Find the property tax and divide that by 12. Divide her insurance by 6. Add all three of those amounts to find how much Destiny pays each month.
Find her payment.
To compute the payment to pay down a loan with beginning principal, P, the payment (pmt) is
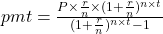 , where r is the annual interest rate (in decimal form), n is the number of compounding periods per year, and t is the number of years. Note, payment to lenders is always rounded up to the next penny.
, where r is the annual interest rate (in decimal form), n is the number of compounding periods per year, and t is the number of years. Note, payment to lenders is always rounded up to the next penny.Once again, it will help you get the right answer from your calculator to find
 first.
first.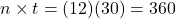
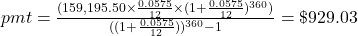
Additional parentheses were added to help you enter the expression properly in your calculator.
Find her property tax.
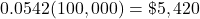
Divide her property tax by 12.
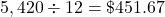
Divide her insurance by 6.
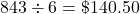
Add the payment, property tax, and insurance to find the monthly payment.
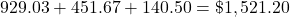
$1,521.20
Try It 6.115
-
Add the amounts to find the gross income.
41,780 + 5,500 = $47,280
$47,280
Try It 6.116
-
Add the deductions: 7,840 + 3,810 + 1,500 = $13,150.
Subtract the legal deductions from the gross income to find the adjustable gross income (AGI).
93,450 – 31,150 = $80,300
The AGI is $80,300.
$80,300
Try It 6.117
-
Exemptions need to be subtracted from the adjusted gross income (AGI) to find the taxable income.
43,100 – 3,400 = $39,700
The taxable income is $39,700.
$39,700
Try It 6.118
-
Add the tax credits.
1,925 + 2,000 = 3,925
Tax credits are subtracted from the tax you owe.
3,950 – 3,925 = $25
The amount of taxes owed after applying tax credits is $25.
$25
Try It 6.119
-
Refund of $1,920
Try It 6.120
-
FICA stands for Federal Insurance Contributions Act of 1935. FICA taxes fund Social Security and Medicare and are automatically withdrawn from your pay. You pay 7.65 percent of your gross pay and your employer matches your amount. Of the 7.65 percent, 6.2 percent goes to Social Security (SSI) and 1.45 percent goes to Medicare. The Social Security (SSI) part only applies to the first $147,000 of your earnings, but the Medicare tax applies to all your gross earnings.
$3,200 per two-week pay period
3,200(26) = $83,200
This is under $147,000, so it is all taxable by both components of FICA.
Find 7.65% of $3,200 to find the FICA contribution.
0.0765(3,200) = $244.80 goes to FICA
Find 6.2% of $3,200 to find the SSI part:
0.062(3,200) = $198.40 to SSI
FICA is $244.80, SSI is $198.40
Try It 6.121
-
FICA stands for Federal Insurance Contributions Act of 1935. FICA taxes fund Social Security and Medicare and are automatically withdrawn from your pay. You pay 7.65 percent of your gross pay and your employer matches your amount. Of the 7.65 percent, 6.2 percent goes to Social Security (SSI) and 1.45 percent goes to Medicare. The Social Security (SSI) part only applies to the first $147,000 of your earnings, but the Medicare tax applies to all your gross earnings.
Only the first $147,000 is taxed for SSI. Ignore the excess.
Find 6.2% of $147,000 to find the SSI part.
0.062(147,000) = $9,114 to SSI
$9,114
Try It 6.122
-
Make your own tax table and write in the taxable income where it belongs in the table.
Add two columns.
Add a column where you subtract the upper income limit from the lower income limit. Notice that in the last row you’ve entered the taxable income for THIS exercise.
In the last column, multiply the amount you just wrote in the fifth column times the tax rate. If you know how to use spreadsheet formulas, you can multiply the cell in column 4 times the cell in column 5 to find the cell in column 6 in Google Sheets.
Delete the rows you are not using.
Add the amounts in the last column to find the total tax paid is $11,787.
Tax Paid: $11,787 Bracket Lower Income Limit Upper Income Limit Tax Rate Upper – Lower (Upper – Lower) × Rate 1 0 $10,275 10% $10,275 $1,028 2 $10,276 $41,775 12% $31,499 $3,780 3 $41,776 $73,500 22% $31,724 $6,979 $11,787
Try It 6.123
-
His credits exceed his taxes owed, so he receives a refund, which is for $1,673.94.
Check Your Understanding
-
To write n% in its fractional form is to write the percent as the fraction
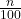 .
.100
100
-
The decimal form of n% is found by calculating the decimal value of n ÷ 100.
38.7% is 38.7 divided by 100.
This moves the decimal point two places to the left, resulting in 0.387.
0.387
-
The formula relating the total (base), the percent in decimal form, and the part (amount) is
 or
or 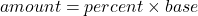 .
.68% of 280

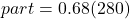
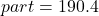
190.4
-
The formula relating the total (base), the percent in decimal form, and the part (amount) is
 .
.342 is 41% of the total.
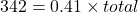
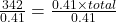
The total is approximately 834.15 (rounded to two decimal places).
834.15 (rounded to two decimal places)
-
The formula relating the total (base), the percent in decimal form, and the part (amount) is
 .
.80,000,000 is what percent of 332,403,650?
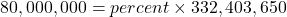
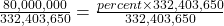
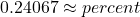
To convert the number x from decimal form to percent, multiply x by 100 and place a percent sign, %, after the number: (x × 100)%.
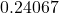 ≈ 24.07% (an approximation)
≈ 24.07% (an approximation)24.07%
-
The formula relating the total (base), the percent in decimal form, and the part (amount) is
 or
or 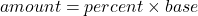 .
.What is 20% of 80?

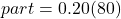
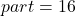
Amazon needs 16 more drivers.
16 new drivers will be hired.
-
a reduction in price
-
the amount a retailer adds to the cost of goods to cover overhead and profit
-
discount = percent discount × original price
discount = 0.32 × 45 = $14.40
sale price = original price – discount
sale price = 45 – 14.40 = $30.60
The price after the discount is $30.60.
$30.60
-
markup = percent markup × cost
markup = 0.60 × $311
markup = $186.60
retail price = cost + markup
retail price = 311 + 186.60 = $497.60
The price after the markup is $497.60.
$497.60
-
Yes.
This pair of formulas mirrors each other.
retail price = cost + markup
total price = purchase price + sales tax
This is another pair of formulas:
markup = percent markup × cost
sales tax = purchase price × tax rate
Yes
-
sales tax = purchase price × tax rate
sales tax = 39.95 × 0.068
sales tax = $2.72 (rounded to the nearest cent) total price = purchase price + sales tax = 39.95 + 2.72 = $42.67
The total price is $42.67.
$42.67
-
Interest is money paid by a borrower to a lender for the privilege of borrowing money.
-
The amount borrowed is the principal.
-
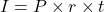
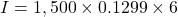
The interest is $1,169.10.
$1,169.10
-
Interest on the loan after 25 days:
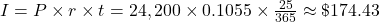
(rounded to the nearest cent) Subtract the partial interest off the loan payment.
$13,000 – 174.43 = $12,825.57 went toward paying off the loan.
$24,200 – 12,825.57 = $11,374.43 is the remaining balance of the loan still due.
$11,374.87
-
The amount of monthly payments, A, for a loan with principal P, monthly simple interest rate r (in decimal form), for t number of months is found using the formula
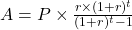 . The monthly interest rate is the annual interest rate divided by 12.
. The monthly interest rate is the annual interest rate divided by 12.4 years = 48 months
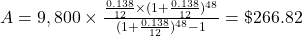
$266.82
-
The present value, PV, of money deposited at an annual, simple interest rate of r (in decimal form) for time t (in years) with a specified future value of FV is calculated with the formula
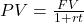 . Present value, in this calculation, is always rounded up. Otherwise, the future value may fall short of the target future value.
. Present value, in this calculation, is always rounded up. Otherwise, the future value may fall short of the target future value.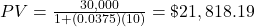
(rounded up to the next cent) $21,818.19
-
interest that is earned on both the principal and the interest from previous periods
-
compound
-
The future value of an investment,
 , when the principal,
, when the principal, 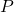 , is invested at an annual interest rate of
, is invested at an annual interest rate of  (in decimal form), compounded
(in decimal form), compounded 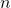 times per year for
times per year for 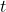 years is found using the formula
years is found using the formula 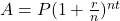 .
.Hint: Find
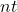 before you plug numbers into your calculator!
before you plug numbers into your calculator! 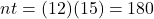 It will help you get the right results. Use those parentheses in your calculator, too!
It will help you get the right results. Use those parentheses in your calculator, too!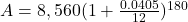
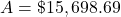
$15,698.69
-
Future value with simple interest:
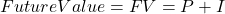
The interest
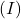 is the principal
is the principal 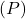 times the annual simple interest rate as a decimal
times the annual simple interest rate as a decimal 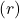 times the time in years
times the time in years 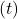 .
.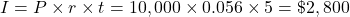
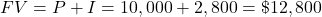
Future value with compound interest:
The future value of an investment,
 , when the principal,
, when the principal, 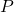 , is invested at an annual interest rate of
, is invested at an annual interest rate of  (in decimal form), compounded
(in decimal form), compounded 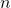 times per year for
times per year for 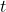 years is found using the formula
years is found using the formula 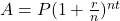 .
.Hint: Find
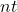 before you plug numbers into your calculator!
before you plug numbers into your calculator! 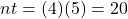 It will help you get the right results. Use those parentheses in your calculator, too!
It will help you get the right results. Use those parentheses in your calculator, too!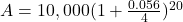
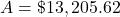
The difference between the two methods:
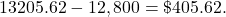
You earn $405.62 more by compounding.
$405.62
-
The money invested in an account bearing an annual interest rate of
 (in decimal form), compounded
(in decimal form), compounded  times per year for
times per year for  years, is called the present value,
years, is called the present value, 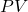 , of the account (or of the money) and found using the formula
, of the account (or of the money) and found using the formula 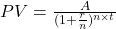 where
where  is the value of the account at the investment’s end. Always round this value up to the next penny.
is the value of the account at the investment’s end. Always round this value up to the next penny.Hint: Find
 before you plug numbers into your calculator!
before you plug numbers into your calculator! 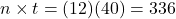
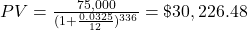
$30,266.48
-
Compare their effective annual yield.
-
Effective annual yield is
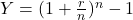 where
where  effective annual yield,
effective annual yield,  the interest rate in decimal form, and
the interest rate in decimal form, and  the number of times the interest is compounded in a year.
the number of times the interest is compounded in a year. 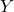 is interpreted as the equivalent annual simple interest rate.
is interpreted as the equivalent annual simple interest rate.
Effective annual yield: 4.98%
4.98%
-
A budget is an estimation of income and expenses over some period of time.
-
Necessary expenses include basic living requirements and debt services such as mortgage/rent, utilities, car, insurance, health care, groceries, gasoline, child care, and minimum debt payments.
Expenses that represent basic living requirement and debt service.
-
Income Amount Expenses Amount Job $3,450.00 Rent $925.00 Car payment $178.54 Car insurance $129.49 Credit card $117.00 Gas $195.00 Food $290.00 Amazon Prime $21.99 Internet $49.99 Going out $400.00 Total $2,307.01 -
Income = $3,450
Expenses
Budget
He has $1,142.99 after accounting for expenses.
$1,142.99
-
The 50-30-20 principle suggests spending 50 percent of your budget on necessary expenses (basic living requirements and debt services such as mortgage/rent, utilities, car, insurance, health care, groceries, gasoline, child care, and minimum debt payments), 30 percent of your budget for wants (restaurants, vacations, hobby costs), and 20 percent should be set aside (retirement funds, stocks, an emergency fund should have at least 3 months of income, other investments).
Monthly income is $3,450.
50% Needs 30% Wants 20% Set Aside Goal $1,725.00 $1,035.00 $690.00 Actual Rent: $925.00
Car payment: $178.54
Car insurance: $129.49
Credit card: $117
Gas: $195.00
Food: $290.00
Total: $1,835.03Amazon Prime: $21.99
Going out: $400.00
Internet: $49.99
Total: $471.98Unused: $1,142.99 David should allocate $1,735 to necessary expenses, $1,035 to expenses that are wants, and $690 to savings and extra debt service.
-
David spends $1,835.03 on necessary expenses, which is fairly close to the 50-30-20 budget philosophy guidelines. He spends $471.98 on expenses that are wants, which is well below the guideline of $1,035. He has $1,149.99 in extra income, which is well above the savings and debt service guidelines.
-
A deposit account, held at a bank or other financial institution, which bears some interest on the deposited money.
-
Once money is deposited in a CD (certificate of deposit), the money cannot be withdrawn until the end of the CD period. Money can be withdrawn from a savings account at any time. Some savings accounts do have a limit to the number of withdrawals per month before a penalty is assessed.
Once money is deposited in a CD, the money cannot be withdrawn until the end of the CD period.
-
A money market account is more flexible. Transactions can be made after creating the money market account.
-
The future value of an investment, A, when the principal, P, is invested at an annual interest rate of r (in decimal form), compounded n times per year for t years is found using the formula
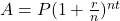 .
.Hint: Find nt before you plug numbers into your calculator!
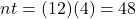
It will help you get the right results. Use those parentheses in your calculator, too!
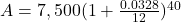
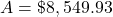
$8,549.93
-
The return on investment (ROI) is the percent difference between the initial investment (P) and the final value of the investment (FV), or
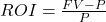 , expressed as a percentage. The length of time of the investment is not considered in ROI.
, expressed as a percentage. The length of time of the investment is not considered in ROI.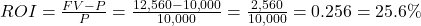
25.6%
-
$21,441.03
The future value of an ordinary annuity is
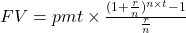 , where FV is the future value of the annuity, pmt is the payment, r is the annual interest rate (in decimal form), n is the number of compounding periods per year, and t is the number of years. It is important to note that the number of deposits per year and the number of compounding periods per year must be the same.
, where FV is the future value of the annuity, pmt is the payment, r is the annual interest rate (in decimal form), n is the number of compounding periods per year, and t is the number of years. It is important to note that the number of deposits per year and the number of compounding periods per year must be the same.It will help you get the right answer using your calculator to find
 first.
first.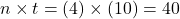
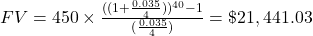
The extra parentheses were added to help you enter the expression properly in your calculator.
-
$2,030.65
To compute the payment to reach a final goal, the payment (pmt) of an ordinary annuity to reach a specific future value (FV) is
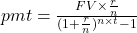 , where r is the annual interest rate (in decimal form), n is the number of compounding periods per year, and t is the number of years. Round up!
, where r is the annual interest rate (in decimal form), n is the number of compounding periods per year, and t is the number of years. Round up!Once again, it will help you get the right answer using your calculator to find
 first.
first.
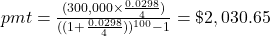
Additional parentheses were added to help you enter the expression properly in your calculator.
-
Stocks are the highest risk of what was studied in the lesson. Bonds, stocks, and mutual funds tend to offer higher returns, but to varying degrees, come with higher risks.
Bonds are considered a conservative investment. They are bought for what is known as the issue price. The interest is fixed (does not change) at the time of purchase and is based on the issue price of the bond. The interest rate is often referred to as the coupon rate; the interest paid is often called the coupon yield. The interest paid is often higher than savings accounts and the risk is exceptionally low.
Stocks are part ownership in a company. They come in units called shares. The performance and earnings of stocks is not guaranteed, which makes them riskier than any other investment discussed earlier. However, they can offer higher return on investment than the other investments. An important thing to remember is that stocks might provide a very large return on investment, but the trade-off is the risk associated with owning stocks.
A mutual fund is a collection of investments that are all bundled together. When you buy shares of a mutual fund, your money is pooled with the assets of other investors. Because there are many different investments inside the mutual fund, the risk is reduced significantly, compared to direct ownership of stocks.
Your employer may offer a retirement account to you. These are often in the form of a 401(k) account. There are traditional and Roth 401(k) accounts, which differ in how they are taxed, much as with other IRAs. These accounts are similar to mutual funds, in that the money is invested in a wide range of assets, spreading the risk.
Stocks
-
Income must be below a threshold for a person to use a Roth IRA.
-
They invest in different investment vehicles so that no single investment can have a large impact on the value of the mutual fund.
-
Use your knowledge of percents. Remember to convert the percentage to a decimal.

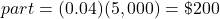
Each year, they receive $200 for 10 years.
Over the 10 years, they receive
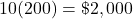 in total.
in total.Each year, the holder of the bond receives $200. For 10 years, that’s $2,000 total earned with the bond.
-
Yes. The limit changes each year. In 2022, a single person’s modified adjusted gross income must be below $129,000 to be eligible for a Roth IRA to be able to make a maximum contribution. This person’s income is below that limit.
Yes
-
Find 4% of $87,500.
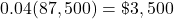
Merisol can deposit up to $3,500 for her employer to match the amount. If she deposits more, the employer will not match it.
$3,500, which is 4% of her income
-
300 shares times $0.38 per share
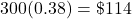
The person earns $114.
$114.00
-
The annual return
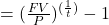 , where t is the number of years, FV is the new value, and P is the starting principal. Convert the answer to a percent.
, where t is the number of years, FV is the new value, and P is the starting principal. Convert the answer to a percent.annual return
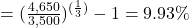
David’s annual return on that investment was 9.93%.
9.93%
-
To compute the payment to reach a final goal for an annuity or mutual fund, the payment (pmt) is
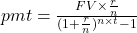 , where r is the annual interest rate (in decimal form), n is the number of compounding periods per year, and t is the number of years. Round up!
, where r is the annual interest rate (in decimal form), n is the number of compounding periods per year, and t is the number of years. Round up!Once again, it will help you get the right answer using your calculator to find
 first.
first.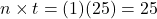
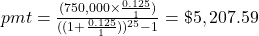
Additional parentheses were added to help you enter the expression properly in your calculator.
The annual payment must be $5,207.59.
$5,207.59
-
Varies
-
Loan with a fixed period, and the borrower pays a fixed amount per period until the loan is paid off
-
More is applied to the principal.
-
The amount of interest, I, to be paid for one period of a loan with remaining principal, P, is
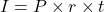 , where r is the interest rate in decimal form, n is the number of payments in a year, and t is the time in years.
, where r is the interest rate in decimal form, n is the number of payments in a year, and t is the time in years.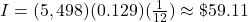
$59.11
-
To compute the payment to pay down a loan with beginning principal, P, the payment (pmt) is
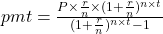 , where r is the annual interest rate (in decimal form), n is the number of compounding periods per year, and t is the number of years. Note, payment to lenders is always rounded up to the next penny.
, where r is the annual interest rate (in decimal form), n is the number of compounding periods per year, and t is the number of years. Note, payment to lenders is always rounded up to the next penny.Once again, it will help you get the right answer from your calculator to find
 first.
first.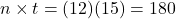
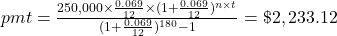
$2,233.12
-
In the seventh row, you see the label “Month” in the first column and “Balance” in the last column. Scroll down to 11 in the Month column. While in that row, look across to the Balance column to see the balance for the Month 11 is $42,962.51.
$42,962.51
-
The cost of finance is the sum of all interest and any fees paid for the loan. Add that to the interest.
$39,544.50
-
Spring (March) before the start of the fall term
-
9 years
-
The difference between the cost of college (including books, fees, room and board, etc.) and all non-loan financial aid they receive
-
In subsidized loans, the interest does not accrue while the student is still in school. In unsubsidized student loans, the interest begins accruing as soon as the money is disbursed.
-
$31,000
-
The amount due for a loan, A, when the principal, P, an interest rate of r (in decimal form), compounded n times per year for t years is found using the formula
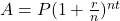 .
.You are told the number of compounding periods.
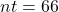
Use those parentheses in your calculator, too!
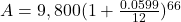
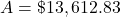
$13,028.61
-
10 years
-
10%
-
Bank issued, store issued, charge (Travel/entertainment) cards
-
Store issued
-
Due date, minimum payment due, and balance due
-
The interest charge, I, for a credit card during a billing cycle is
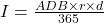 , where ADB is the average daily balance, r is the annual percentage rate as a decimal, and d is the number of days in the billing cycle. As before, interest is rounded up to the next penny.
, where ADB is the average daily balance, r is the annual percentage rate as a decimal, and d is the number of days in the billing cycle. As before, interest is rounded up to the next penny.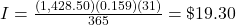
$19.30
-
Use a list of transactions.
Step 1: Create a table that has the sum of transactions for each day. Expenditures are positive. Payments are negative.
Step 2: Add a column, “Days Until Balance Changed,” where you write the number of days until the balance changed. This is the difference between the date of this row and the next.
Step 3: Add a column, “Balance Times Days,” where you multiply the previous two columns.
Date Activity Transaction Balance Days Until Balance Changed Balance Times Days 15-Jun Balance $3,825.50 $3,825.50 5 $19,127.50 20-Jun Food/Clothing $470.31 $4,295.81 9 $38,662.29 29-Jun Payment –$750.00 $3,545.81 2 $7,091.62 1-Jul Restaurant $94.80 $3,640.61 5 $18,203.05 6-Jul Gas/Repair/Int $783.68 $4,424.29 4 $17,697.16 10-Jul Cell/Food $260.24 $4,684.53 5 $23,422.65 Step 4: Sum the last column.
$124,204.27
Step 5: Divide the sum by the number of days in the month. This is the average daily balance.
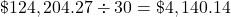
The average daily balance (ADB) is $4,140.14.
$4,104.27
-
$696.21
First, find the interest.
The interest charge, I, for a credit card during a billing cycle is
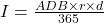 , where ADB is the average daily balance, r is the annual percentage rate as a decimal, and d is the number of days in the billing cycle. As before, interest is rounded up to the next penny.
, where ADB is the average daily balance, r is the annual percentage rate as a decimal, and d is the number of days in the billing cycle. As before, interest is rounded up to the next penny.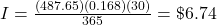
Add the interest to the balance at the end of the billing cycle.
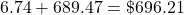
-
Cost of delivering the vehicle to the dealer
-
Registers your car with the state, gets the license plate, and assigns the title of the car to the lender
-
To compute the payment to pay down a loan with beginning principal, P, the payment (pmt) is
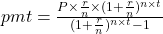 , where r is the annual interest rate (in decimal form), n is the number of compounding periods per year, and t is the number of years. Note, payment to lenders is always rounded up to the next penny.
, where r is the annual interest rate (in decimal form), n is the number of compounding periods per year, and t is the number of years. Note, payment to lenders is always rounded up to the next penny.Once again, it will help you get the right answer from your calculator to find
 first.
first.
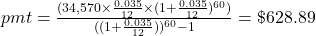
Additional parentheses were added to help you enter the expression properly in your calculator.
$628.89
-
Interest rate higher loan term shorter
-
Title and registration, documentation fee, sales tax
-
There are 36 months in 3 years.
The monthly depreciation for a car, MD, is
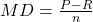 , where P is the price paid for the car, R is the residual value of the car, and n is the number of months of the lease.
, where P is the price paid for the car, R is the residual value of the car, and n is the number of months of the lease.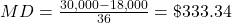
$333.34
-
3.75%
The annual percentage rate (APR) is APR = 2400 × MF, where MF is the money factor of the lease and the APR is calculated as a decimal.
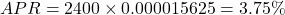
-
Purchasing
-
Cover the damage caused to your car if involved in an accident with another vehicle
-
Buying
-
Renting
-
Buying
-
Mortgage
-
To compute the payment to pay down a loan with beginning principal, P, the payment (pmt) is
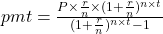 , where r is the annual interest rate (in decimal form), n is the number of compounding periods per year, and t is the number of years. Note, payment to lenders is always rounded up to the next penny.
, where r is the annual interest rate (in decimal form), n is the number of compounding periods per year, and t is the number of years. Note, payment to lenders is always rounded up to the next penny.Once again, it will help you get the right answer from your calculator to find
 first.
first.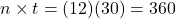
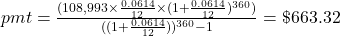
Additional parentheses were added to help you enter the expression properly in your calculator.
$663.32
-
In the previous exercise, you found the monthly payment was $663.32.
The total paid, T, on a t year mortgage with monthly payments pmt is
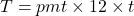 .
.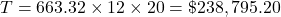
The total paid is $238,795.20.
Subtract the cost of the house from the total paid to find the cost of financing.
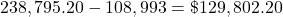
$129,802.20
-
Look at the seventh row. You see the label “Month” in the first column and “Principal” in the third column. Go down to the row for Month 141 and you will see $554.06 in the Principal column.
$554.06
-
Escrow
-
Any and all income, including wages, salary, interest earned, gifts, and winnings
-
After deductions are subtracted
-
Add the deductions: 2,000 + 3,000 + 8,000 = 13,000.
Subtract the legal deductions from the gross income to find the adjustable gross income (AGI).
50,000 – 13,000 = $37,000
The AGI is $37,000.
$37,000
-
After taxes are calculated, credits are subtracted from taxes owed.
-
No, only for up to $147,000
-
Make your own tax table and write in the taxable income where it belongs in the table.
Add two columns.
Add a column where you subtract the upper income limit from the lower income limit. Notice that in the last row you’ve entered the taxable income for THIS exercise. If you know how to use spreadsheet formulas, you can have Google Sheets do the subtraction.
In the last column, multiply the amount you just wrote in the fifth column times the tax rate. If you know how to use spreadsheet formulas, you can multiply the cell in column 4 times the cell in column 5 to find the cell in column 6 in Google Sheets.
Add the amounts in the last column to find the total tax paid is $4,812.66 or $4,813 if you round.
Delete the rows you are not using.
Did you know that when you e-file taxes, the amount you pay is always rounded to dollars?
Tax Owed: $4,812.66 Bracket Lower Income Limit Upper Income Limit Tax Rate Upper – Lower (Upper – Lower) * Rate 1 0 $10,275 10% $10,275 $1,027.50 2 $10,276 $41,775 12% $31,499 $3,779.88 3 $41,776 $41,800 22% $24 $5.28 $4,813
-
Subtract the tax credits to find the amount of tax owed.
5,600 – 4,000 = $1,600
$1,600
