Ch. 7 Review Exercises – Algebra and Trigonometry 2e | OpenStax
Angles
For the following exercises, convert the angle measures to degrees.
For the following exercises, convert the angle measures to radians.
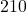
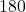
- Find the length of an arc in a circle of radius 7 meters subtended by the central angle of
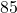 .
. - Find the area of the sector of a circle with diameter 32 feet and an angle of
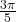 radians.
radians.
For the following exercises, find the angle between ![]() and
and ![]() that is coterminal with the given angle.
that is coterminal with the given angle.
For the following exercises, find the angle between 0 and ![]() in radians that is coterminal with the given angle.
in radians that is coterminal with the given angle.
For the following exercises, draw the angle provided in standard position on the Cartesian plane.
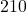
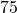
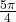
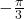
- Find the linear speed of a point on the equator of the earth if the earth has a radius of 3,960 miles and the earth rotates on its axis every 24 hours. Express answer in miles per hour. Round to the nearest hundredth.
- A car wheel with a diameter of 18 inches spins at the rate of 10 revolutions per second. What is the car’s speed in miles per hour? Round to the nearest hundredth.
Right Triangle Trigonometry
For the following exercises, use side lengths to evaluate.
For the following exercises, use the given information to find the lengths of the other two sides of the right triangle.
For the following exercises, use Figure 1 to evaluate each trigonometric function.
For the following exercises, solve for the unknown sides of the given triangle.
- A 15-ft ladder leans against a building so that the angle between the ground and the ladder is
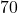 . How high does the ladder reach up the side of the building? Find the answer to four decimal places.
. How high does the ladder reach up the side of the building? Find the answer to four decimal places. - The angle of elevation to the top of a building in Baltimore is found to be 4 degrees from the ground at a distance of 1 mile from the base of the building. Using this information, find the height of the building. Find the answer to four decimal places.
Unit Circle
- Find the exact value of
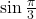 .
. - Find the exact value of
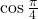 .
. - Find the exact value of
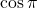 .
. - State the reference angle for
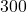 .
. - State the reference angle for
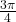 .
. - Compute cosine of
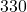 .
. - Compute sine of
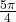 .
. - State the domain of the sine and cosine functions.
- State the range of the sine and cosine functions.
The Other Trigonometric Functions
For the following exercises, find the exact value of the given expression.
For the following exercises, use reference angles to evaluate the given expression.
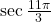
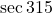
- If
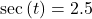 , what is the
, what is the 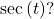
- If
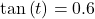 , what is the
, what is the 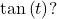
- If
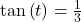 , find
, find 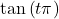 .
. - If
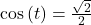 , find
, find 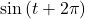 . There are two possible solutions.
. There are two possible solutions. - Which trigonometric functions are even?
- Which trigonometric functions are odd?
