Tree Diagrams, Tables, and Outcomes

1. If you draw a card at random from a standard 52-card deck and note its suit, what is the sample space?
2. If you draw 2 cards at random from a standard 52-card deck and note the 2 suits (without paying attention to the order), what is the sample space?
3. If you draw 2 Scrabble tiles in order without replacement from a bag containing E, E, L, S, what is the sample space?
4. If you draw 2 Scrabble tiles without replacement and ignoring order from a bag containing E, E, L, S, what is the sample space?
5. If you draw 2 Scrabble tiles without replacement and ignoring order from a bag containing E, E, L, S, what is the sample space?
6. If you draw 2 Scrabble tiles with replacement and ignoring order from a bag containing E, E, L, S, what is the sample space?

Basic Concepts of Probability

7. If you read that the probability of flipping 10 heads in a row is 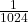, is that probability most likely theoretical, empirical, or subjective?
8. If someone tells you that there is a 40% chance that a Democrat wins the U.S. Presidential election in 2132, is that probability most likely theoretical, empirical, or subjective?
9. If your professor says that you have a 20% chance of getting an A in her class because 20% of her students historically have earned As, is that probability most likely theoretical, empirical, or subjective?

In the following exercises, you are about to roll a standard 12-sided die (with faces labeled 1–12).

10. What is the probability of rolling a negative number?
11. What is the probability of rolling a number less than 20?
12. What is the probability of rolling an 11?
13. What is the probability of rolling a number less than 7?
14. What is the probability of not rolling an 11?
15. What is the probability of rolling a multiple of 4?
16. Over the last 30 years, it has rained 12 times on May 1. What empirical probability would you assign to the event “it rains next May 1”?

Probability with Permutations and Combinations

In the following exercises, you’re drawing cards from a special deck of cards containing 2♡, 2♣, 2♢, 2♠, 3♡, 3♣, 3♠, 4♡, 4♣, 5♡.

17. If you draw 4 cards without replacement, what is the probability of drawing a 2, 3, 4, and 5 in order?
18. If you draw 4 cards without replacement, what is the probability of drawing a 2, 3, 4, and 5 in any order?
19. If you draw 3 cards without replacement, what is the probability that you draw a ♡, a ♣, and a ♡, in order?
20. If you draw 3 cards without replacement, what is the probability that you draw 2 ♡ and 1 ♣, in any order?

What Are the Odds?

21. If you roll a standard 20-sided die (with faces numbered 1–20), what are the odds against rolling a number less than 5?
22. If you roll a standard 20-sided die (with faces numbered 1–20), what are the odds in favor of rolling greater than a 5?
23. If 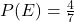, what are the odds in favor of ?
24. If 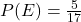, what are the odds against ?

The Addition Rule for Probability

In the following exercises, you’re drawing a single card from a special deck of cards containing 2♡, 2♣, 2♢, 2♠, 3♡, 3♣, 3♠, 4♡, 4♣, 5♡.

25. What is the probability of drawing a 2 or a 3?
26. What is the probability of drawing a ♣ or a ♠?
27. What is the probability of drawing a 2 or a ♡?
28. What is the probability of drawing an even number or a ♣?

Conditional Probability and the Multiplication Rule

In the following exercises, you’re drawing from a special deck of cards containing 2♡, 2♣, 2♢, 2♠, 3♡, 3♣, 3♠, 4♡, 4♣, 5♡.

29. If you draw a single card, what is:
    1. P(draw a 2)
    2. P(draw a 2 | draw a ♡)
    3. P(draw a 2 | draw a ♠)
30. If you draw a single card, what is:
    1. P(draw a ♡)
    2. P(draw a ♡ | draw a 3)
    3. P(draw a ♡ | draw a 2)

In the following exercises, you are playing the following game that involves rolling 2 dice, one at a time. First, you roll a standard 6-sided die. If the result is a 4 or less, your second roll uses a standard 4-sided die. If the result of the first roll is a 5 or 6, your second roll uses a standard 6-sided die. Find these probabilities:

31. P( first roll is a 3 and second roll is a 3 )
32. P(first roll is a 6 and second roll is a 6 )
33. P(second roll is a 6 )
34. P( second roll is a 1 )

Each of the following exercises involve drawing a Scrabble tile from a bag. These tiles are labeled with a letter and a point value, as follows: A(1), C(3), D(2), E(1), E(1), J(8), K(5), O(1), R(1), R(1).

1. How many ways are there to draw a vowel and then a consonant from the bag?
2. How many ways are there to draw a tile worth an even number of points and then a tile worth an odd number of points from the bag?
3. How many ways are there to draw 4 tiles from the bag without replacement, if order matters?
4. How many ways are there to draw 4 consonants from the bag without replacement, if order matter?
5. How many ways are there to draw 4 tiles from the bag with replacement, if order does not matter?
6. How many ways are there to draw 4 consonants from the bag with replacement, if order does not matter?
7. Give the sample space of the experiment that asks you to draw 2 tiles from the bag with replacement and note their point values, where order doesn’t matter. Give the outcomes as ordered pairs.
8. Give the sample space of the experiment that asks you to draw 2 tiles from the bag without replacement and note their point values, where order doesn’t matter. Give the outcomes as ordered pairs.
9. If you draw a single tile from the bag, what is the probability that it’s an E?
10. If you draw a single tile from the bag, what is the probability that it’s not an A?
11. If you draw 3 tiles from the bag without replacement, what is the probability that they spell RED, in order?
12. If you draw 3 tiles from the bag without replacement, what is the probability that they spell RED, in any order?
13. What are the odds against drawing a vowel?
14. Use your answer to question 12 to find the odds against drawing three tiles without replacement and being able to spell RED.
15. If you draw one tile, what is the probability of drawing a J or a K?
16. If you draw one tile, what is the probability that it’s a vowel or that it’s worth more than 4 points?
17. Suppose you’re about to draw one tile from the bag. Find 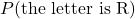and .
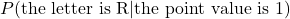18. If you draw 2 tiles with replacement, what is the probability of drawing a consonant first and then a vowel?
19. If you draw 2 tiles without replacement, what is the probability of drawing a consonant first and then a vowel?
20. If you draw 10 tiles with replacement, what is the probability that you draw exactly 3 vowels? Round to 3 decimal places.
21. If you draw 100 tiles with replacement, what is the probability that you draw fewer than 35 vowels? Round to 4 decimal places.
22. Find and interpret the expected number of points on the tile, assuming you draw 1 tile from the bag.
23. Find the expected sum of points on 2 tiles, selected without replacement.
24. If your friend offers you a bet where they pay you $10 if you draw a vowel from the bag, but you owe them $5 if you draw a consonant, should you take it? How do you know?

Text Attribution

This text was adapted from Chapter 7 Review of Contemporary Mathematics, textbooks originally published by OpenStax.