1.2 Subsets
Learning Objectives
After completing this section, you should be able to:
- Represent subsets and proper subsets symbolically.
- Compute the number of subsets of a set.
- Classify a real number as a natural, whole, integer, rational, or irrational number.
- Subsets of the set of real numbers.
Subsets
Set 𝐴 is a subset of set 𝐵 if every member of set 𝐴 is also a member of set 𝐵. Symbolically, this relationship is written as 𝐴⊆𝐵.
Sets can be related to each other in several different ways: they may not share any members in common; they may share some members in common, or they may share all members in common. In this section, we will explore the way we can select a group of members from the whole set.
Every set is also a subset of itself, 𝐵⊆𝐵
Let A be a set of all odd natural numbers less then 7 and let B be a set of natural numbers that are less then 7. We will use the roster notation to represent the sets:
A= {1, 3, 5}, B= {1, 2, 3, 4, 5, 6,}, The set A is a subset of set B, because every member or element of set A is also a member of set B. More specifically, set A is a proper subset of set B, because there are other members of set B not in set A. This is written as A⊂B. The only subset of a set that is not a proper subset of the set would be the set itself.
The empty set or null set, ∅, is a proper subset of every set, except itself.
Graphically, sets are often represented as circles. In the following graphic, set 𝐴 is represented as a circle completely enclosed inside the circle representing set 𝐵, showing that set 𝐴 is a proper subset of set 𝐵. The element 𝑥 represents an element that is in both set 𝐴 and set 𝐵.
While we can list all the subsets of a finite set, it is not possible to list all the possible subsets of an infinite set, as it would take an infinitely long time.
Example 1
Set 𝐿 is a set of reading materials available in a shop at the airport, L = {a, b, c}. List all the subsets of set L.
Show / Hide Solution
Step 1: It is best to begin with the set itself, as every set is a subset of itself. In our example, the cardinality of set 𝐿
is 𝑛(𝐿)=3. There is only one subset of set 𝐿 that has the same number of elements of set 𝐿: {a, b, c}.
Step 2: Next, list all the proper subsets of the set containing 𝑛(𝐿)−1 elements. In this case, 3−1=2. There are three subsets that each contain two elements: {a, b}, {a, c}, and {b, c}.
Step 3: Continue this process by listing all the proper subsets of the set containing 𝑛(𝐿)−2
elements. In this case, 3−2=1. There are three subsets that contain one element: {a}, {b}, and {c}.
Step 4: Finally, list the subset containing 0 elements, or the empty set: {}.
Try It 1
Consider the set of possible outcomes when you flip a coin, 𝑆={heads, tails}. List all the possible subsets of set 𝑆.
Show / Hide Solution
{}, {heads}, {tails}, {heads, tails}
Example 2
Consider the set of all one-digit numbers, P.
Determine if the following sets are proper subsets of P.
- 𝑀= {1, 3, 7, 8}
- 𝐺= {0}
- 𝑉= {1, 2, 3, 4, 5, 6, 7, 8, 9}
Show / Hide Solution
𝑀 is a proper subset of 𝑃, written symbolically as 𝑀⊂𝑃 because every member of 𝑀 is a member of set 𝑃, but 𝑃 also contains at least one element that is not in 𝑀. 𝐺 is a single member proper subset of 𝑃, written symbolically as 𝐺⊂𝑃, because Green is a member of set 𝑃, but 𝑃 also contains other members (such as Democratic) that are not in 𝐺. 𝑉 is subset of 𝑃 because every member of 𝑉 is also a member of 𝑃, but it is not a proper subset of 𝑃 because there are no members of 𝑉 that are not also in set 𝑃. We can represent the relationship symbolically as 𝑉⊆𝑃, or more precisely, set 𝑉 is equal to set 𝑃, 𝑉=𝑃.
Try It 2
Consider the set of all whole numbers less then 8. Give an example of a proper subset containing:
- One member
- Three members
- No members
Show / Hide Solution
- Ther are multiple possible solutions. Ex: {5]
- Ther are multiple possible solutions. Ex: {0, 4,6]
- {}
A standard deck of 52 cards has the following characteristics:
- 4 suits (hearts, diamonds, spades, and clubs)
- Two suits are red (hearts and diamonds) and two black (spades and clubs)
- Each suit has 13 cards
- Face cards are Jacks, Queens, and Kings
Example 3
Consider the subsets of a standard deck of cards: 𝑆 = {spades, hearts, diamonds, clubs}; 𝑅 = {hearts, diamonds}; 𝐵 = {spades, clubs}; and 𝐶={clubs}.
Express the relationship between the following sets symbolically.
- Set 𝑆 and set 𝐵
- Set 𝐶 and set 𝐵
- Set 𝑅 and 𝑅
Show / Hide Solution
- 𝐵⊂𝑆. 𝐵 is a proper subset of set 𝑆.
- 𝐶⊂𝐵. 𝐶 is a proper subset of set 𝐵.
- 𝑅⊆𝑅 or 𝑅=𝑅. 𝑅 is subset of itself, but not a proper subset of itself because 𝑅 is equal to itself.
Try it 2
Express the relationship between the set of natural numbers, ![]() and the set of even numbers,
and the set of even numbers, ![]() .
.
Show / Hide Solution
They are disjoint sets.
Exponential Notation
So far, we have figured out how many subsets exist in a finite set by listing them. Recall that in Example 1.11, when we listed all the subsets of the three-element set ![]() we saw that there are eight subsets. In Your Turn 1.11, we discovered that there are four subsets of the two-element subset, 𝑆={heads, tails}.
we saw that there are eight subsets. In Your Turn 1.11, we discovered that there are four subsets of the two-element subset, 𝑆={heads, tails}.
A one-element set has two subsets, the empty set and itself. The only subset of the empty set is the empty set itself. But how can we easily figure out the number of subsets in a very large finite set? It turns out that the number of subsets can be found by raising 2 to the number of elements in the set, using exponential notation to represent repeated multiplication. For example, the number of subsets of the set 𝐿{newspaper, magazine, book} is equal to ![]() .
.
Exponential notation is used to represent repeated multiplication, ![]() , where 𝑏 appears as a factor 𝑛 times.
, where 𝑏 appears as a factor 𝑛 times.
The number of subsets of a finite set A is equal to 2 raised to the power of 𝑛(𝐴), where 𝑛(𝐴) is the number of elements in set 𝐴:
![]()
Note that ![]() , so this formula works for the empty set, also.
, so this formula works for the empty set, also.
Example 4
Find the number of subsets of each of the following sets.
- The set of top five scorers of all time in the NBA: 𝑆={LeBron James, Kareem Abdul-Jabbar, Karl Malone, Kobe Bryant, Michael Jordan}.
- The set of the top four bestselling albums of all time: 𝐴={Thriller, Hotel California, The Beatles White Album, Led Zepplin IV}.
- 𝑅={Snap, Crackle, Pop}.
Show / Hide Solution
- 𝑛(𝑆)=5. So, the total number of subsets of S is
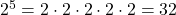 .
. - 𝑛(𝐴)=4. Therefore, the toal number of subsets of A is
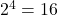 .
. - 𝑛(𝑅)=3. So, the total number of subsets of R is
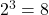
Try It 4
Compute the total number of subsets in the set of the top nine tennis grand slam singles winners, 𝑇={Margaret Court, Serena Williams, Steffi Graff, Rafael Nadal, Novak Djokovic, Roger Federer, Helen Wills, Martina Navratilova, Chris Everett}.
Show / Hide Solution
512
Classifying Real Numbers
In the last subchapter, we defined the set of integers adds the opposites of the natural numbers to the set of whole numbers: ![]() .
.
It is useful to note that the set of integers is made up of three distinct subsets: negative integers, zero, and positive integers. In this sense, the positive integers are just the natural numbers. Another way to think about it is that the natural numbers are a subset of the integers.
…,−3,−2,−1,negative integers0,zero1,2,3,⋯positive integers
The set of is defined as ![]() .
.
Notice from the definition that rational numbers are fractions (or quotients) containing integers in both the numerator and the denominator, and the denominator is never 0. We can also see that every natural number, whole number, and integer is a rational number with a denominator of 1.
Because they are fractions, any rational number can also be expressed as a terminating or repeating decimal. Any rational number can be represented as either:
ⓐ a terminating decimal: ![]() ,
,
or
ⓑ a repeating decimal: ![]()
We use a line drawn over the repeating block of numbers instead of writing the group multiple times.
Example 5
Write each of the following rational numbers as either a terminating or repeating decimal.
- -5 / 7
- 15 / 5
- 13 /25
Show / Hide Solution
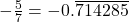 , a repeating decimal
, a repeating decimal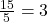 , a terminating decimal
, a terminating decimal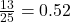 , a terminating decimal
, a terminating decimal
Try it 5
Write each of the following rational numbers as either a terminating or repeating decimal.
- 68 / 17
- 8 / 13
- −17 / 20
Show / Hide Solution
- 4
- 0.615384 repeating
- -0.85
Irrational Numbers
At some point in the ancient past, someone discovered that not all numbers are rational numbers. A builder, for instance, may have found that the diagonal of a square with unit sides was not 2 or even 3 / 2, but was something else. Or a garment maker might have observed that the ratio of the circumference to the diameter of a roll of cloth was a little bit more than 3, but still not a rational number. Such numbers are said to be irrational because they cannot be written as fractions. These numbers make up the set of irrational numbers. Irrational numbers cannot be expressed as a fraction of two integers. It is impossible to describe this set of numbers by a single rule except to say that a number is irrational if it is not rational. So we write this as shown.
Example 6
Determine whether each of the following numbers is rational or irrational. If it is rational, determine whether it is a terminating or repeating decimal.
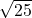
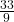
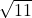
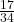
- 0.3033033303333
Show / Hide Solution
- This can be simplified as
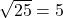 . Therefore, it is rational.
. Therefore, it is rational. - Because it is a fraction of integers, it is a rational number. Next, simplify and divide.
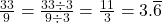
- It is irrational because 11 is not a perfect square and
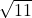 cannot be expressed as a fraction.
cannot be expressed as a fraction. - It is rational because it is a fraction of integers. Next, simplify it to show it is rational and a terminating integer.
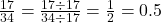
- 0.3033033303333… is not a terminating decimal. Also note that there is no repeating pattern because the group of 3s increases each time. Therefore it is neither a terminating nor a repeating decimal and, hence, not a rational number. It is an irrational number.
Try it 6
Determine whether each of the following numbers is rational or irrational. If it is rational, determine whether it is a terminating or repeating decimal.
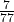
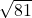
- 4.27027002700027…
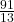
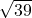
Show / Hide Solution
- rational
- rational
- irrational
- rational
- irrational
Real Numbers
Given any number n, we know that n is either rational or irrational. It cannot be both. The sets of rational and irrational numbers together make up the set of real numbers. As we saw with integers, the real numbers can be divided into three subsets: negative real numbers, zero, and positive real numbers. Negative and positive real numbers include fractions, decimals, and irrational numbers according to their algebraic sign (+ or –). Zero is considered neither positive nor negative.
The real numbers can be visualized on a horizontal number line with an arbitrary point chosen as 0, with negative numbers to the left of 0 and positive numbers to the right of 0. A fixed unit distance is then used to mark off each integer (or other basic value) on either side of 0. Any real number corresponds to a unique position on the number line.The converse is also true: Each location on the number line corresponds to exactly one real number. This is known as a one-to-one correspondence. We refer to this as the real number line as shown in Figure 1.
Example 7
Write true or false.
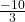
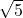
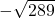
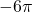
- 0.615384615384…
Show / Hide Solution
- This is negative and rational. It lies to the left of 0 on the number line.
- This is positive and irrational. It lies to the right of 0.
- This is negative and rational. It lies to the left of 0.
- This is negative and irrational. It lies to the left of 0.
- This is a repeating decimal, so it is rational and lies to the right of 0.
Try it 7
Classify each number as either positive or negative and as either rational or irrational. Does the number lie to the left or the right of 0 on the number line?
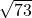
- −11.411411411…
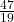
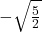
- 6.210735
Show / Hide Solution
- positive and rational
- negative and rational
- positive and rational
- negative and irrational
- positive and rational
Sets of Numbers as Subsets
Beginning with the natural numbers, we have expanded each set to form a larger set, meaning that there is a subset relationship between the sets of numbers we have encountered so far. These relationships become more obvious when seen as a diagram, such as Figure 2.
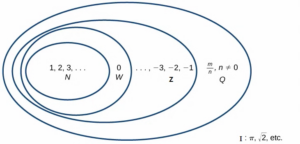
Sets of Numbers
N: The set of natural numbers includes the numbers used for counting: ![]()
W: The set of whole numbers is the set of natural numbers plus zero: ![]()
Z: The set of integers adds the negative natural numbers to the set of whole numbers: ![]() .
.
Q: The set of rational numbers includes fractions written as ![]() .
.
The set of irrational numbers is the set of numbers that are not rational, are nonrepeating, and are nonterminating: I= {ℎ|ℎ is not a rational number}.
Example 8
Classify each number as being a natural number (N), whole number (W), integer (Z), rational number (Q), and/or irrational number (I).
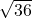
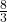
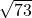
- −6
- 3.2121121112
Show / Hide Solution
- N, W, I, Q
- Q
- I
- Z, Q
- I
Try it 8
Classify each number as being a natural number (N), whole number (W), integer (Z), rational number (Q), and/or irrational number (I).
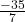
- 0
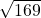
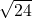
- 4.763763763…
Show / Hide Solution
- Z, Q
- W, Z, Q
- N, W, Z, Q
- I
- Q
Examples 9
Write true or false
- Z⊆R
- W⊆N
- I⊆Q
- N⊂N
Show / Hide Solution
- True
- False
- False
- False
Try it 9
Write true or false
- I⊆R
- W⊆Q
- Z⊆N
- Q⊂Q
Show / Hide Solution
1. True
2. True
3. False
4. False
1.2 Exercise Set
- Every member of a ________ of a set is also a member of the set.
- Explain what distinguishes a proper subset of a set from a subset of a set.
- The _______ set is a proper subset of every set except itself.
- Is the following statement true or false? 𝐴⊆𝐴.
- If the cardinality of set 𝐴 is 𝑛(𝐴)=10, then set 𝐴 has a total of ___________ subsets.
- Set 𝐴 is ______________ to set 𝐵 if 𝑛(𝐴) = 𝑛(𝐵).
- If every member of set 𝐴 is a member of set B and every member of set B is also a member set 𝐴, then set 𝐴 is ____________ to set 𝐵.
Exercise Set 1-7 Answers
- subset
- To be a subset of a set, every member of the subset must also be a member of the set. To be a proper subset, there must be at least one member of the set that is not also in the subset.
- empty
- true
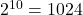
- equivalent
- Equal sets have the same elements. For each set, there can be no element that is not an element of the other set. Sets A and B are equal because every member of A is in B and every member of B is in A.
For the following exercises, list all the proper subsets of each set.
- {chocolate, vanilla, strawberry}
- {true, false}
- {mother, father, daughter, son}
- {7}
For the following exercises, determine the relationship between the two sets and write the relationship symbolically.
![]()
- D and 𝐴
- B and 𝐷
- 𝐶 and 𝐷
- Z and 𝐶
- 𝑍 and ∅
- A and 𝐵
- A and 𝐶
- ∅ and D
- B and 𝐶
- 𝐴 and 𝑍
For the following exercises, calculate the total number of subsets of each set.
- {Adele, Beyonce, Cher, Madonna, Shakira}
- {Art, Paul}
- {Peter, Paul, Mary}
- ∅
- {3}
- {𝑙,𝑜,𝑣,𝑒}
- {}
- Set 𝐴, if n(𝐴) = 12.
- Set 𝐵, if 𝑛(𝐵)=9.
For the following exercises, use the set of letters in the word largest as the set, 𝑈={l, a, r, g, e, s, t}.
- Find a subset of 𝑈 that is equivalent, but not equal, to the set:
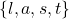 .
. - Find a subset of 𝑈 that is equal to the set:
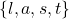 .
. - Find a subset of 𝑈 that is equal to the set:
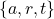 .
. - Find a subset of 𝑈 that is equivalent, but not equal, to the set:
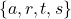 .
. - Find a subset of 𝑈 that is equivalent, but not equal, to the set:
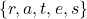 .
. - Find a subset of 𝑈 that is equal to the set:
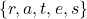 .
. - Find two three-character subsets of set 𝑈 that are equivalent, but not equal, to each other.
- Find two three-character subsets of set 𝑈 that are equal to each other.
- Find two five-character subsets of set 𝑈 that are equal to each other.
- Find two five-character subsets of set 𝑈 that are equivalent, but not equal, to each other.
For the following exercises, use the set of integers as the set ![]() .
.
- Find two equivalent subset of 𝑈 with a cardinality of 7.
- Find two equal subsets of 𝑈 with a cardinality of 4.
- Find a subset of 𝑈 that is equivalent, but not equal to,
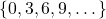 .
. - Find a subset of 𝑈 that is equivalent, but not equal to,
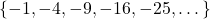 .
. - True or False. The set of natural numbers,
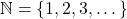 , is equivalent to set 𝑈.
, is equivalent to set 𝑈. - True or False. Set 𝑈 is an equivalent subset of the set of rational numbers,
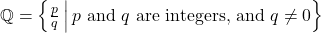 .
.
Attributions
Text Attribution
This text was adapted from Chapter 1.2 of Contemporary Mathematics, textbooks originally published by OpenStax.
