2.3 Permutations with Restrictions and Repetitions

imazur

2.3 Permutations with Restrictions and Repetitions

Learning Objectives

After completing this section, you should be able to:

Determine the number of permutations with restrictions.
Determine the number of permutations with repetitions.
Apply permutations to solve problems.

Permutations with Restrictions

When solving problems with restrictions using the fundamental counting principle, remember to deal with restrictions first.

Example 1

In how many ways can you arrange all the letters of the word GAMES, if

there are no restrictions
the first letter must be E

Answer the questions using the fundamental counting principle and factorials

Show / Hide Solution

$5 \times 4 \times 3 \times 2 \times 1 = 120$ ; $5! = 120$
$1 \times 4 \times 3 \times 2 \times 1 = 24$ ; $4! = 24$

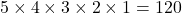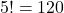
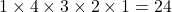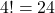
Try It 1

In how many ways can you arrange all the letters of the word FRIDAY, if

there are no restrictions
the first letter must be D

Answer the questions using the fundamental counting principle and factorials

Show / Hide Solution

$6 \times 5 \times 4 \times 3 \times 2 \times 1 = 720$ ; $6! = 720$
$1 \times 5 \times 4 \times 3 \times 2 \times 1 = 120$ ; $5! = 120$

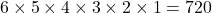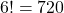
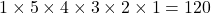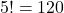
Example 2

Two parents and three children are lined up to take a family photo. In how many ways they can line up if;

there are no restrictions
children and parents will alternate
children are together

Show / Hide Solution

$5! = 120$
$3!2! = 12$
$3!3! = 36$

Try It 2

Two parents and five children are lined up to take a family photo. In how many ways they can line up if;

there are no restrictions
parents are together
children are together

Show / Hide Solution

$7! = 5040$
$2!6! = 1440$
$5!3! = 720$

Example 3

Find the number of permutations of the letters in the word TRIANGLE if:

the letters RNE must be together in that order
the letters RNE must be together but not necessary in that order

Show / Hide Solution

$6! = 720$
$3! \times 6! = 4320$

Try It 3

Find the number of permutations of the letters in the word METHODS if:

the letters TOS must be together in that order
the letters TOS must be together but not necessary in that order

Show / Hide Solution

$5! = 120$
$3! \times 5! = 720$

Permutations with Repetitions

How many arrangements did you end up with?

Example 4

Find the number of arrangements of all letters in word HOME by finishing to list all possible arrangements.

Show / Hide Solution

HOME EHOM MEHO OMEH
HOEM
HMOE
HMEO
HEOM
HEMO
The number of arrangements is $4! = 24$

Try It 4

Find the number of arrangements of all letters in word HOMM by finishing to list all possible arrangements.

Show / Hide Solution

HOMM EMOM MMHO OMMH
HOMM
HMOM
HMMO
HMOM
HMMO
The number of arrangements is $\frac{4!}{2!} = 12$

Example 5

Find the number of arrangements of all letters in word HMMM by listing all possible arrangements.

Show / Hide Solution

$\frac{4!}{3!} = 4$

Try It 5

Find the number of arrangements of all letters in word MMM by listing all possible arrangements.

Show / Hide Solution

$\frac{3!}{3!} = 1$

To find out the number of permutations with repetitions we can use the following formula:

$\frac{n!}{a! b! c!}$ where n is the numbers of objects and a, b, and c are the same objects

Example 6

Find the number of permutations of the letters of the word GRAPHING

Show / Hide Solution

$\frac{8!}{2!} = 20160$

Try It 6

Find the number of permutations of the letters of the word CONDITIONAL

Show / Hide Solution

$\frac{11!}{2! 2! 2!} = 4989600$

Example 7

Find the number of permutations of the letters of the word DISTRIBUTIONS if:

there are no restrictions
the arrangements must begin with R
the arrangements must begin with I
the arrangements must begin with T

Show / Hide Solution

$\frac{13!}{3! 2! 2!} = 259459200$
$\frac{12!}{3! 2! 2!} = 19958400$
$\frac{12!}{2! 2! 2!} = 59875200$
$\frac{12!}{3! 2!} = 39916800$

Try It 7

Find the number of permutations of the letters of the word DIVISIONS

there are no restrictions
the arrangements must begin with V
the arrangements must begin with I
the arrangements must begin with S

Show / Hide Solution

$\frac{9!}{3! 2!} = 30240$
$\frac{8!}{3! 2!} = 3360$
$\frac{8!}{2! 2!} = 10080$
$\frac{8!}{3!} = 6720$

2.3 Exercise Set

How many ways can 5 different books be arranged on a shelf?
In how many different ways can the letters in the word “LAMP” be arranged?
How many 3-digit numbers can be formed using the digits 1, 2, 3, 4, and 5 if no digit is repeated?
How many ways can 6 people be seated in a row of 6 chairs?
How many ways can the first, second, and third prizes be awarded to 10 contestants (no repeats)?
How many distinct permutations are there of the word “LEVEL”?
How many unique arrangements can be made from the letters of the word “MISSISSIPPI”?
How many different 4-letter words (real or not) can be formed using the letters A, B, C, and D, if letters can be repeated?
How many 4-digit numbers can be formed from the digits 1 to 9 such that no digit repeats and the number is even?
From the word “ORANGE”, how many 4-letter arrangements can be made if the letter “O” must be the first letter?
In how many ways can 5 people be arranged in a line if two specific people must sit next to each other?
From the digits 0 to 9, how many 3-digit numbers can be formed where the digits do not repeat and the number does not start with zero?
A password consists of 4 letters followed by 3 digits. How many such passwords can be formed if no letter or digit is repeated?
In how many ways can 8 people be seated around a circular table?
How many 5-letter words can be formed using the letters A, B, C, D, E, F, and G such that the word starts with a vowel and no letter is repeated?