2.2 Factorial Notation and Permutations

imazur

2.2 Factorial Notation and Permutations

Learning Objectives

After completing this section, you should be able to:

Use the Multiplication Rule for Counting to determine the number of permutations.
Compute expressions containing factorials.
Compute permutations.
Apply permutations to solve problems.

Three swimmers are racing in separate lanes in a swimming pool. The swimmer in the top lane is in first place, the swimmer in the bottom lane is in second place, and the swimmer in the middle lane is in third place. — Figure 7.7 – We can use permutations to calculate the number of different orders of finish in an Olympic swimming heat. (credit: “London 2012 Olympics Park Stratford London” by Gary Bembridge/Flickr, CC BY 2.0)

Swimming events are some of the most popular events at the summer Olympic Games. In the finals of each event, 8 swimmers compete at the same time, making for some exciting finishes. How many different orders of finish are possible in these events? In this section, we’ll extend the Multiplication Rule for Counting to help answer questions like this one, which relate to permutations. A permutation is an ordered list of objects taken from a given population. The length of the list is given, and the list cannot contain any repeated items.

Applying the Multiplication Rule for Counting to Permutations

In the case of the swimming finals, one possible permutation of length 3 would be the list of medal winners (first, second, and third place finishers). A permutation of length 8 would be the full order of finish (first place through eighth place). Let’s use the Multiplication Rule for Counting to figure out how many of each of these permutations there are.

EXAMPLE 1

The final heat of Olympic swimming events features 8 swimmers (or teams of swimmers).

How many different podium placements (first place, second place, and third place) are possible?
How many different complete orders of finish (first place through eighth place) are possible?

Show/Hide Solution

Let’s start with the first place finisher. How many options are there? Since 8 swimmers are competing, there are 8 possibilities. Once that first swimmer completes the race, there are 7 swimmers left competing for second place. After the second finisher is decided, there are 6 swimmers remaining who could possibly finish in third place. Thus, there are 8 possibilities for first place, 7 for second place, and 6 for third place. The Multiplication Rule for Counting then tells us there are 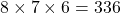$8 \times 7 \times 6 = 336$ different ways the winners’ podium can be filled out.
To look at the complete order of finish, we can continue the pattern we can see in part 1 of this example: There are 5 possibilities for fourth place, 4 for fifth place, 3 for sixth place, 2 for seventh place, and then just 1 swimmer is left to finish in eighth place. Using the Multiplication Rule for Counting, we see that there are 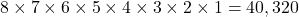$8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1 = 40,320$ possible orders of finish.

TRY IT 1

You have a hand of 5 cards (that happen to create what’s called a royal flush in the game of poker): 10♠, J♠, Q♠, K♠, and A♠. Into how many different orders can you put those cards?

Show/Hide Solution

The Multiplication Rule of Counting says that if there are n ways to accomplish one task and m ways to accomplish a second task, then there are 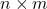$n \times m$ ways to accomplish both tasks. You can tack on additional tasks by multiplying the number of ways to accomplish those tasks to your previous product.

Choosing…	You choose a card for the first position	You choose a card for the second position	You choose a card for the third position	You choose a card for the second position	You choose a card for the last position
Number of Choices	You have 5 choices	You have 4 cards left from which to choose	You have 3 cards left from which to choose	You have 2 cards left from which to choose	You have 1 card left from which to choose

The number of ways you can make your choices is $5 \times 4 \times 3 \times 2 \times 1 = 120$ .

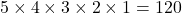Factorials

The pattern we see in Example 1 occurs commonly enough that we have a name for it: factorial.

For any natural number $n$ , we define the factorial of $n$ (denoted $n!$ and read “ $n$ factorial”) to be the product of every natural number less than or equal to $n$ .

$n!$

We also define 0! =1.

We will use factorials in a couple of different contexts, so let’s get some practice doing computations with them.

EXAMPLE 2

Compute the following:

$4!$
$\frac{8!}{6!}$
$\frac{9!}{3!4!}$

Show/Hide Solution

$4! = 4 \times 3 \times 2 \times 1 = 24$
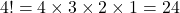
There are two ways to approach this calculation. The first way is to compute the factorials first, then divide: 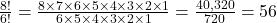$\frac{8!}{6!} = \frac{8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}{6 \times 5 \times 4 \times 3 \times 2 \times 1} = \frac{40,320}{720} = 56$ However, there is an easier way! You may notice in the second step that there are several terms that can be canceled; that’s always the case whenever we divide factorials. In this case, notice that we can rewrite the numerator like this: 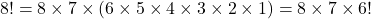$8! = 8 \times 7 \times (6 \times 5 \times 4 \times 3 \times 2 \times 1) = 8 \times 7 \times 6!$ With that in mind, we can proceed this way by canceling out the 6!: 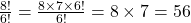$\frac{8!}{6!} = \frac{8 \times 7 \times 6!}{6!} = 8 \times 7 = 56$ That’s much easier!
Let’s approach this one using our canceling technique. When we see two factorials in either the numerator or denominator, we should focus on the larger one first. So: $\frac{9!}{3!4!} = \frac{9 \times 8 \times 7 \times 6 \times 5 \times 4!}{3!4!} = \frac{9 \times 8 \times 7 \times 6 \times 5}{3 \times 2 \times 1} = 9 \times 8 \times 7 \times 5 = 2,520$

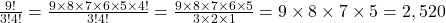
TRY IT 2

Compute the following:

$6!$
$\frac{12!}{10!}$
$\frac{8!}{4!4!}$

Show/Hide Solution

A factorial for any positive whole number n (denoted n!) is the product of every whole number less than or equal to n. We define 0! to be equal to one. $6! = 6 \times 5 \times 4 \times 3 \times 2 \times 1 = 720$
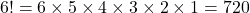
A factorial for any positive whole number n (denoted n!) is the product of every whole number less than or equal to n. We define 0! to be equal to one. 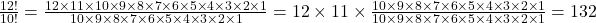$\frac{12!}{10!} = \frac{12 \times 11 \times 10 \times 9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}{10 \times 9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1} = 12 \times 11 \times \frac{10 \times 9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}{10 \times 9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1} = 132$ Instead of writing out all the factors, you could have written this expression an easier way.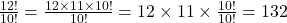 $\frac{12!}{10!} = \frac{12 \times 11 \times 10!}{10!} = 12 \times 11 \times \frac{10!}{10!} = 132$
A factorial for any positive whole number n (denoted n!) is the product of every whole number less than or equal to n. We define 0! to be equal to one. $\frac{8!}{4!4!} = \frac{8 \times 7 \times 6 \times 5 \times 4!}{4! \times 4 \times 3 \times 2 \times 1} = \frac{1,680}{24} = 70$

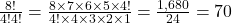
EXAMPLE 3

Simplify:

$\frac{8!}{6!}$

Show/Hide Solution

$\frac{8!}{6!}$ = 56

\frac{8!}{6!} = \frac{8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}{6 \times 5 \times 4 \times 3 \times 2 \times 1}

6 \times 5 \times 4 \times 3 \times 2 \times 1 = 6!

TRY IT 3

Simplify:

$\frac{10!}{7!}$

Show/Hide Solution
720

EXAMPLE 4

$\frac{(n+1)!}{n!}$

Show/Hide Solution
n+1

TRY IT 4

$\frac{n!}{(n-2)!}$

Show/Hide Solution
n(n-1)!

Permutations

As we’ve seen, factorials can pop up when we’re computing permutations. In fact, there is a formula that we can use to make that connection explicit. Let’s define some notation first. If we have a collection of $n$ objects and we wish to create an ordered list of $r$ of the objects (where $1 \leq r \leq n$ ), we’ll call the number of those permutations $_{n}P_{r}$ (read “the number of permutations of $n$ objects taken $r$ at a time”). We formalize the formula we’ll use to compute permutations below.

$_{n}P_{r} = \frac{n!}{(n-r)!}$

If you wondered why we defined $0! = 1$ earlier, it was to make formulas like this one work; if we have $n$ objects and want to order all of them (so, we want the number of permutations of $n$ objects taken $n$ at a time), we get $_{n}P_{n} = \frac{n!}{(n-n)!} = \frac{n!}{0!} = \frac{n!}{1} = n!$ . Next, we’ll get some practice computing these permutations.

EXAMPLE 5

Find the following numbers:

The number of permutations of 12 objects taken 3 at a time
The number of permutations of 8 objects taken 5 at a time
The number of permutations of 32 objects taken 2 at a time

Show/Hide Solution

$_{12}P_{3} = \frac{12!}{(12-3)!} = \frac{12!}{9!} = \frac{12 \times 11 \times 10 \times 9!}{9!} = 12 \times 11 \times 10 = 1,320$
$_{8}P_{5} = \frac{8!}{(8-5)!} = \frac{8 \times 7 \times 6 \times 5 \times 4 \times 3!}{3!} = 8 \times 7 \times 6 \times 5 \times 4 = 6,720$
$_{32}P_{2} = \frac{32!}{(32-2)!} = \frac{32 \times 31 \times 30!}{30!} = 32 \times 31 = 992$

TRY IT 5

Find the following numbers:

The number of permutations of 6 objects taken 2 at a time
The number of permutations of 14 objects taken 4 at a time
The number of permutations of 19 objects taken 3 at a time

Show/Hide Solution

30
24024
5814

EXAMPLE 6

A high school graduating class has 312 students. The top student is declared valedictorian, and the second-best is named salutatorian. How many possible outcomes are there for the valedictorian and salutatorian?
In the card game blackjack, the dealer’s hand of 2 cards is dealt with 1 card faceup and 1 card facedown. If the game is being played with a single deck of (52) cards, how many possible hands could the dealer get?
The University Combinatorics Club has 3 officers: president, vice president, and treasurer. If there are 18 members of the club, how many ways are there to fill the officer positions?

Show/Hide Solution

This is the number of permutations of 312 students taken 2 at a time, and $_{312}P_{2} = 97,032$ .
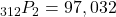We want the number of permutations of 52 cards taken 2 at a time, and $_{52}P_{2} = 2,652$ .
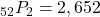Here we’re looking for the number of permutations of 18 members taken 3 at a time, and $_{18}P_{3} = 4,896$ .

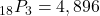TRY IT 6

One of the big draws at this year’s state fair is the pig race. There are 15 entrants, and prizes are given to the top three finishers. How many different arrangements of top three finishes could there be?

Show/Hide Solution

455

Who Knew?

Very Big Permutations

Permutations involving relatively small sets of objects can get very big, very quickly. A standard deck contains 52 cards. So, the number of different ways to shuffle the cards—in other words, the number of permutations of 52 objects taken 52 at a time—is $52! \approx 8 \times 10^{67}$ (written out, that’s an 8 followed by 67 zeroes). The estimated age of the universe is only about $4 \times 10^{17}$ seconds. So, if a very bored all-powerful being started shuffling cards at the instant the universe began, it would have to have averaged at least $\frac{8 \times 10^{67}}{4 \times 10^{17}} \approx 2 \times 10^{50}$ shuffles per second since the beginning of time to have covered every possible arrangement of a deck of cards. That means the next time you pick up a deck of cards and give it a good shuffle, it’s almost certain that the particular arrangement you created has never been created before and likely never will be created again.

Check your understanding

Compute 5!.
Compute $\frac{10!}{7!3!}$ .
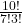Compute $_{12}P_{3}$ .
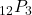Compute $_{8}P_{4}$ .
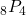The standard American edition of the board game Monopoly has a deck of 15 orange Chance cards. In how many different ways could the first 4 Chance cards drawn in a game appear?

Show / Hide Solution

$5! = 120.$
$.$

2.2 Exercise Set

3!
9!
$\frac{7!}{2!2!3!}$
$\frac{8!}{5!2!}$
$\frac{21!}{18!2!}$
$\frac{28!}{26!2!}$
$\frac{34!}{30!3!}$
$\frac{17!}{12!5!}$
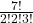
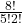
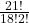
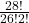
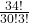
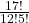
The following exercises are about the card game euchre, which uses a partial standard deck of cards: It only has the cards with ranks 9, 10, J, Q, K, and A for a total of 24 cards. Some variations of the game use the 8s or the 7s and 8s, but we’ll stick with the 24-card version.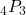
$_{4}P_{3}$
$_{7}P_{5}$
$_{12}P_{10}$
$_{14}P_{10}$
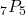
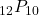
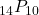
The following exercises involve a horse race with 13 entrants.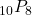
$_{10}P_{8}$
$_{15}P_{11}$
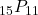
A euchre hand contains 5 cards. How many ways are there to receive a 5-card hand (where the order in which the cards are received matters, i.e., 9♡, J♡, K♣, 9♠, 10♠ is different from 9♠ J♡, 9♡, K♣, 10♠)?
After all 4 players get their hands, the remaining 4 cards are placed facedown in the center of the table. How many arrangements of 4 cards are there from this deck?
Euchre is played with partners. How many ways are there for 2 partners to receive 5-card hands (where the order in which the cards are received matters)?
How many different arrangements of the full euchre deck are possible (i.e., how many different shuffles are there)?
How many possible complete orders of finish are there?
An exacta bet is one where the player tries to predict the top two finishers in order. How many possible exacta bets are there for this race?
A trifecta bet is one where the player tries to predict the top three finishers in order. How many possible trifecta bets are there for this race?
A superfecta bet is one where the player tries to predict the top four finishers in order. How many possible superfecta bets are there for this race?