1.1 Basic Set Concepts

 

Learning Objectives

After completing this section, you should be able to:

  • Represent sets in a variety of ways.
  • Represent well-defined sets and the empty set with proper set notation.
  • Compute the cardinal value of a set.
  • Differentiate between finite and infinite sets.

Sets and Ways to Represent Them

Let us think about the English alphabet as a set; then all letters of the alphabet are elements in that set. Sets can be described in several different ways: by roster notation, by set-builder notation, by interval notation, by graphing on a number line, and by Venn diagrams. Sets are typically designated with capital letters. The simplest way to represent a set with only a few members is the roster (or listing) notation, in which the elements in a set are listed, enclosed by curly braces and separated by commas.

For larger sets that have a natural ordering, sometimes an ellipsis is used to indicate that the pattern continues. It is common practice to list the first three elements of a set to establish a pattern, write the ellipsis, and then provide the last element. Consider the set of all lowercase letters of the English alphabet, A. This set can be written symbolically as A = \{a, b, c, \dots, z\}.

 

Example 1

Write a set consisting of all vowels using roster notation and label it with a capital V.

 

Show / Hide Solution

V={a, e, i, o, u}

Think about math alphabet and how do we create numbers. What symbols do we use to represent numbers?

A digit is a symbol used in mathematics to represent numbers.

 

Try It 1

Write a set consisting of all digits and label it with a capital D.

Show / Hide Solution

D = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}

Using digits, we can create any number. How many numbers do we have?  Knowing that a finite set has a limited or fixed number of elements, is the set finite?

Do you remember any set of numbers that you were using in mathematics?

Our number system is made up of several different infinite sets of numbers. The first sets of numbers are set of natural numbers and whole numbers. We use an ellipsis for infinite sets, which have an unlimited number of elements, to indicate that the pattern continues.

In set theory:

The set of natural numbers, which is the set of all positive counting numbers, is represented as \mathbb{N} = \{1, 2, 3, \dots\}

It is denoted with the symbol N.

The set of whole numbers incudes all natural numbers plus zero, is \mathbb{W} = \{0, 1, 2, 3, \dots\}.

It is denoted with the symbol W.

Notice that for those sets, there is no element following the ellipsis. This is because there is no largest natural or whole number; you can always add one more to get to the next natural or whole number. Because the set of natural and whole numbers grows without bound, they are infinite sets.

The set of integers is another infinite set of numbers.

The set of integers incudes all whole numbers and their opposites and it is denoted with the symbol Z.

There is no largest or smallest integer.

Example 2

Write the set of integers using the roster notation and label it with a ℤ.

 

Show / Hide Solution

 

Step 1: As always, we write the label and then the opening bracket. Because the negative counting numbers are infinite, to represent that the pattern continues without bound to the left, we must use an ellipsis as the first element in our list.

Step 2: We place a comma and follow it with at least three consecutive integers separated by commas to establish a pattern.

Step 3: Add an ellipsis to the end of the list to show that the set of integers continues without bound to the right.

Complete the list with a closing bracket. The set of integers may be represented as follows: \mathbb{Z} = \{ \ldots, -2, -1, 0, 1, 2, \ldots \}.

Try It 2

Write the set of odd natural numbers greater than 0 and label it with a capital 𝑀.

Show / Hide Solution

M = { 1, 3, 5, …}

Example 3

Write the set of even natural numbers including and between 2 and 100, and label it with a capital E. Include an ellipsis.

 

Show / Hide Solution

Write the label, 𝐸 followed by an equal sign and then a bracket. Write the first three even numbers separated by commas, beginning with the number two to establish a pattern. Next, write the ellipsis followed by a comma and the last number in the list, 100. Finally, write the closing bracket to complete the set.

Write the label, 𝐸 followed by an equal sign and then a bracket.

 

E={

Write the first three even numbers separated by commas, beginning with the number 2 to establish a pattern.

 

E={2,4,6,

Next, write the ellipsis followed by a comma and the last number in the list, 100.

 

E={2,4,6,…,100

Finally, write the closing bracket to complete the set.

 

𝐸={2,4,6,…,100}

Try It 3

Use an ellipsis to write the set of single digit numbers greater than or equal to zero and label it with a capital 𝐷.

Show / Hide Solution

D = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}

All the sets we have considered so far have been well-defined sets.

A well-defined set clearly communicates whether an element is a member of the set or not.

 

Consider the following examples.

Examples 4

For each of the following sets, determine if it represents a well-defined set.

  1. A group of first five whole numbers.
  2. A group of five important integers.
Show / Hide Solution
  1. The group of five first whole numbers is a well-defined set, because you can clearly identify if any number is or is not an element of that group. For example, 5 is not an element of this set, but 4 is an element of this set.
  2. A group of five integers is not a well-defined set because the word important is ambiguous. Some people might consider a 0 as an important number, while others might think 13 is. Because people can disagree on what is and what is not an element of this group, the set is not well-defined.

Try It 4

For each of the following collections, determine if it represents a well-defined set.

  1. A group of first four even natural numbers.
  2. A group of four great natural numbers.
Show / Hide Solution
  1. It represents well-defined set.
  2. It does not represent well-defined set.

If we were to consider the set of all negative natural numbers, this set would be known as an empty set; the number of elements in this set is 0, since there were no negative counting numbers.

The empty set, also called the null set, does not have any elements in it. The set is written symbolically using a pair of braces, { } or a zero with a slash through it, ∅.

The set containing the number 0, {0},is a set with one element in it. It is not the same as the empty set, {} which does not have any elements in it. Symbolically: {0}≠ { }.

Example 5

Natural numbers that have only two unique divisors, 1 and itself is called prime numbers. Represent the following sets symbolically.

  1. The set of prime numbers less than 2.
  2. The set of birds that are also mammals.

 

Show / Hide Solution
  1. A prime number is a natural number greater than 1 that is only divisible by one and itself. Since there are no prime numbers less than 2, this set is empty, and we can represent it symbolically as follows: {} or ∅. These two different symbols for the empty set can be used interchangeably.
  2. The set of birds and the set of mammals do not intersect, so the set of birds that are also mammals is empty, and we can represent it symbolically as ∅ or {}.

Try It 5

Represent the set of all numbers divisible by 0 symbolically.

Show / Hide Solution

{} or ∅.

 

Number Zero

We use the number zero to represent the concept of nothing every day. The machine language of computers is binary, consisting only of zeros and ones, and even way before that, the number zero was a powerful invention that allowed our understanding of mathematics and science to develop. The historical record shows the Babylonians first used zeros around 300 B.C., while the Mayans developed and began using zero separately around 350 A.D. What is considered the first formal use of zero in arithmetic operations was developed by the Indian mathematician Brahmagupta around 650 A.D.

See Brahmagupta, Mathematician and Astronomer [biography] on the Story of Mathematics (n.d.) website.

Another interesting feature of the number zero is that although it is an even number, it is the only number that is neither negative nor positive.

 

In all the above definitions of sets of numbers we used the roster method to represent them. A shorthand way to write sets is with the use of, which is a verbal description or formula for the set. For example, the set of all lowercase letters of the English alphabet, 𝐴 written in set builder notation is:

A = \{ x \mid x \text{ is a lowercase letter of the English alphabet} \}

This is read as, “Set 𝐴 is the set of all elements 𝑥 such that 𝑥 is a lowercase letter of the English alphabet.”

In that notation we define the elements of a set by stipulating criteria ie. {x| x meets a certain criteria}. The criteria could be stated using words, numerals, or symbols.

Example 6

Write the set of natural numbers using the set-builder notation.

Show / Hide Solution

{x | x ∈ N}

 

Try it 6

Write the set of integers using the set builder notation.

Show / Hide Solution

{x | x ∈ Z}

Computing the Cardinal Value of a Set

Almost all the sets most people work with outside of pure mathematics are finite sets. For these sets,

The cardinal value or cardinality of the set is the number of elements in the set. For finite set 𝐴, the cardinality is denoted symbolically as 𝑛(𝐴).

 

For example, a set that contains four elements has a cardinality of 4.

How do we measure the cardinality of infinite sets? The ‘smallest’ infinite set is the set of natural numbers, or counting numbers, \mathbb{N} = \{1, 2, 3, \dots\}.

 

This set has a cardinality of \aleph_0 (pronounced “aleph-null”). All sets that have the same cardinality as the set of natural numbers are countably infinite. This concept, as well as notation using aleph, was introduced by mathematician Georg Cantor who once said, “A set is a Many that allows itself to be thought of as a One.”

Example 7

Write the cardinal value of each of the following sets in symbolic form.

  1. F = {f, g, h, i}
  2. The empty set.
Show / Hide Solution

There are 5 distinct elements in set 𝐹. Therefore, the cardinal value of set 𝐹 is 5 and written symbolically as 𝑛(𝐹)=5.

Because the empty set does not have any elements in it, the cardinality of the empty set is zero. Symbolically we write this as: 𝑛(∅)=0.

 

Try It 7

Write the cardinal value of each of the following sets in symbolic form.

  1. Set 𝑃 is the set of prime numbers less than 2.
  2. Set A is the set of lowercase letters of the English alphabet, 𝐴={a,b,c,d,e, f, g}.
Show / Hide Solution
  1. 𝑛(∅)=0.
  2. 𝑛(A)=7

Now that we have learned to represent finite and infinite sets using both the roster method and set builder notation, we should also be able to determine if a set is finite or infinite based on its verbal or symbolic description. One way to determine if a set is finite or not is to determine the cardinality of the set. If the cardinality of a set is a natural number, then the set is finite.

Example 8

Classify each of the following sets as infinite or finite.

  1. E = {2, 4, 6, 8, 10}
  2. 𝐴 is the set of lowercase letters of the English Alphabet, A = {a, b, c, dots, z}.
  3. \mathbb{Q} = \left\{ \frac{p}{q} \,\middle|\, p \text{ and } q \text{ are integers, and } q \ne 0 \right\}
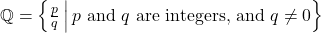
Show / Hide Solution
  1. n(E) = 5. Since 5 is a natural number, the set is finite.
  2. n(A) = 26. Since 26 is a natural number, the set is finite.
  3. Set ℚ is the set of rational numbers or fractions. Because the set of integers is a subset of the set of rational numbers, and the set of integers is infinite, the set of rational numbers is also infinite. There is no smallest or largest rational number.

Try It 8

Classify each of the following sets as infinite or finite.

  1. B = {b, a, k, e}
  2. \mathbb{W} = \{ x \mid x \text{ is a whole number} \}
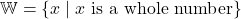
Show / Hide Solution
  1. The set B is finite.
  2. The set W is infinite.

 

People in Mathematics

A portrait of Georg Cantor.
George Cantor (unknown author/Wikimedia) Public Domain

Georg Cantor

Georg Cantor, the father of modern set theory, was born during the year 1845 in Saint Petersburg, Russia and later moved to Germany as a youth. Besides being an accomplished mathematician, he also played the violin. Cantor received his doctoral degree in Mathematics at the age of 22.

In 1870, at the age of 25 he established the uniqueness theorem for trigonometric series. His most significant work happened between 1874 and 1884, when he established the existence of transcendental numbers (also called irrational numbers) and proved that the set of real numbers are uncountably infinite—despite the objections of his former professor Leopold Kronecker.

Cantor published his final treatise on set theory in 1897 at the age of 52, and was awarded the Sylvester Medial from the Royal Society of London in 1904 for his contributions to the field. At the heart of Cantor’s work was his goal to solve the continuum problem, which later influenced the works of David Hilbert and Ernst Zermelo.

 

 

Video:

 

Check your understanding

  1. A _____________ is a well-defined collection of objects.
  2. The _________________ of a finite set 𝐴, denoted n (A), is the number of elements in set 𝐴.
  3. Determine if the following description describes a well-defined set: “The top 5 pizza restaurants in Kelowna.”
  4. The United States is the only country to have landed people on the moon as of March 21, 2021. What is the cardinality of the set of all people who have walked on the moon prior to this date?
  5. Is the set of all butterflies in the world a finite set or an infinite set?
  6. Represent the set of all upper-case letters of the English alphabet using both the roster notation and set builder notation.
Questions 1-5 Answers
  1. set
  2. cardinality
  3. not a well- defined set
  4. 0
  5. infinite set
  6. A= {A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V,W,X,Y,Z}, A= \{ x \mid x \text{ is a an upper-case letter of English alphabet} \}

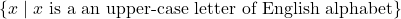
1.1 Exercise Set

For the following exercises, represent each set using roster notation.

  1. The set of primary colors: red, yellow, and blue.
  2. The set of natural numbers between 50 and 100.
  3. The set of natural numbers greater than 17.
  4. The set of natural numbers less than 21.

For the following exercises, represent each set using set builder notation.

  1. The set of all integer multiples of 3 that are greater than zero.
  2. The set of all integer multiples of 4 that are greater than zero.
  3. The set of all plants that are edible.
  4. The set of all even numbers.

For the following exercises, compute the cardinal value of each set.

  1. P = \{\text{Snuzzle}, \text{Butterscotch}, \text{Blue Belle}, \text{Minty}, \text{Blossom}, \text{Cotton Candy}\}
  2. T = \{\text{pepperoni}, \text{sausage}, \text{bacon}, \text{ham}, \text{mushrooms}, \text{olives}, \text{bell pepper}, \text{pineapple}\}
  3. ∅
  4. B = \{5, 6, 7, \dots, 20\}
  5. F = \left\{ \frac{1}{9}, \frac{2}{9}, \frac{3}{9}, \frac{4}{9}, \frac{5}{9}, \frac{6}{9}, \frac{7}{9}, \frac{8}{9}, \frac{9}{9} \right\}
  6. {}
  7. L = \{l, m, n, \dots, y\}
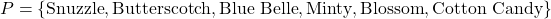
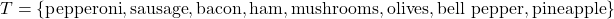
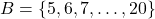
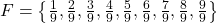
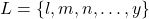
  8. The set of numbers on a standard 6-sided die.

For the following exercises, determine if the set described is finite or infinite.

  1. The set of natural numbers.
  2. The empty set.
  3. The set consisting of all jazz venues in Vancouver, British Columbia.
  4. The set of all real numbers.
  5. The set of all different types of cheeses.
  6. The set of all words in Merriam-Webster’s Collegiate Dictionary, Eleventh Edition, published in 2020.

 

1.1 Answers:

  1. {red,yellow,blue}

  2. {51,52,53,…,99}

  3. {18,19,20,21,…

  4. \{ 1, 2, 3, 4, \dots, 20 \}{x∣x=3n,n∈N}

  5. {x∣x=4n,n∈N}

  6. {x∣xis a plant andxis edible}

  7. {x∣x=2n,n∈Z}\{ x \mid x = 2n, \, n \in \mathbb{Z} \}

  8. P={Snuzzle,Butterscotch,Blue Belle,Minty,Blossom,Cotton Candy}P = \{\text{Snuzzle}, \text{Butterscotch}, \text{Blue Belle}, \text{Minty}, \text{Blossom}, \text{Cotton Candy}\}

    n(P)=6n(P) = 6

  9. T={pepperoni,sausage,bacon,ham,mushrooms,olives,bell pepper,pineapple}

    n(T)=8n(T) = 8

  10. \emptyset

    n(∅)=0n(\emptyset) = 0

  11. n(B)=16n(B) = 16

  12. F = \left\{ \frac{1}{9}, \frac{2}{9}, \frac{3}{9}, \frac{4}{9}, \frac{5}{9}, \frac{6}{9}, \frac{7}{9}, \frac{8}{9}, \frac{9}{9} \right\}n(F) = 9

  14. From l through yn(L) = 14

  15. \{1, 2, 3, 4, 5, 6\}

    n=6n = 6

  16. infinite
  17. finite
  18. finite
  19. infinite
  20. finite
  21. finite

Attributions

Text Attribution

This text was adapted from Chapter 1.1 of Contemporary Mathematics, textbooks originally published by OpenStax.

Media Attribution

References

Akihiro Kanamori, “Set Theory from Cantor to Cohen,” Editor(s): Dov M. Gabbay, Akihiro Kanamori, John Woods, Handbook of the History of Logic, North-Holland, Volume 6, 2012.

Brahmagupta: Mathematician and astronomer. (n.d.). Story of Mathematics. https://www.storyofmathematics.com/indian_brahmagupta.html/

Wikipedia contributors. “Cantor.” Wikipedia, The Free Encyclopedia, 23 Mar. 2021. Web. 20 Jul. 2021.

License

Foundations of Mathematics 12 Copyright © by imazur. All Rights Reserved.

Share This Book