1.4 Set Operations with Two Sets
Learning Objectives
After completing this section, you should be able to:
- Determine the intersection of two sets.
- Determine the union of two sets.
- Determine the cardinality of the union of two sets.
- Apply the concepts of AND and OR to set operations.
- Draw conclusions from Venn diagrams with two sets.
The movie Yours, Mine, and Ours was originally released in 1968 and starred Lucille Ball and Henry Fonda. This movie, which is loosely based on a true story, is about the marriage of Helen, a widow with eight children, and Frank, a widower with ten children, who then have an additional child together. The movie is a comedy that plays on the interpersonal and organizational struggles of feeding, bathing, and clothing twenty people in one household.
If we consider the set of Helen’s children and the set of Frank’s children, then the child they had together is the intersection of these two sets, and the collection of all their children combined is the union of these two sets. In this section, we will explore the operations of union and intersection as it relates to two sets.
The Intersection of Two Sets
The members that the two sets share in common are included in the intersection of two sets.
To be in the intersection of two sets, an element must be in both the first set and the second set. In this way, the intersection of two sets is a logical AND statement. Symbolically, 𝐴 intersection 𝐵 is written as: 𝐴∩𝐵. 𝐴 intersection 𝐵 is written in set builder notation as: ![]() .
.
EXAMPLE 1
Set ![]() .
.
Find 𝐴 intersection .
Show / Hide Solution
The intersection of sets 𝐴 and 𝐵 include the elements that set 𝐴 and 𝐵 have in common: 3, 5, and 7. ![]()
TRY IT 1
Set ![]() and
and ![]() . Find 𝐴 intersection 𝐵.
. Find 𝐴 intersection 𝐵.
Show / Hide Solution
{5}
Notice that if sets 𝐴 and 𝐵 are disjoint sets, then they do not share any elements in common, and 𝐴 intersection 𝐵 is the empty set, as shown in the Venn diagram below.
EXAMPLE 2
Set 𝐴={0,2,4,6,8} and set 𝐵={1,3,5,7,9}.
Find 𝐴∩𝐵.
Show / Hide Solution
Because sets 𝐴 and 𝐵 are disjoint, they do not share any elements in common. So, the intersection of set 𝐴 and set 𝐵 is the empty set. 𝐴∩𝐵=∅.
TRY IT 2
Set 𝐴={3, 5, 7} and set 𝐵={4, 6, 8}. Find 𝐴∩𝐵.
Show / Hide Solution
{}
Notice that if set 𝐴 is a subset of set 𝐵, then 𝐴 intersection 𝐵 is equal to set 𝐴, as shown in the Venn diagram below.
EXAMPLE 3
Set 𝐴={1,3,5,…} and set 𝐵=ℕ={1,2,3,…}. Find 𝐴∩𝐵.
Show / Hide Solution
Because set 𝐴 is a subset of set 𝐵, 𝐴 intersection 𝐵 is equal to set 𝐴. 𝐴∩𝐵=𝐴={1,3,5,…}, the set of odd natural numbers.
TRY IT 3
Set 𝐴={𝑎,𝑏,𝑐,…,𝑧} and set 𝐵={𝑎,𝑒,𝑖,𝑜,𝑢}. Find 𝐴∩𝐵.
Show / Hide Solution
{a, e, i, o, u}
The Union of Two Sets
Like the union of two families in marriage, the union of two sets includes all the members of the first set and all the members of the second set.
To be in the union of two sets, an element must be in the first set, the second set, or both. In this way, the union of two sets is a logical inclusive OR statement. Symbolically, 𝐴 union 𝐵 is written as: 𝐴∪𝐵.
EXAMPLE 4
Set 𝐴={1,3,5,7,9} and set 𝐵={2,3,5,7}. Find 𝐴 union 𝐵.
Show / Hide Solution
𝐴 union 𝐵 is the set formed by including all the unique elements in set 𝐴, set 𝐵, or both sets 𝐴 and 𝐵: 𝐴∪𝐵={1,3,5,7,9,2}.
The first five elements of the union are the five unique elements in set 𝐴. Even though 3, 5, and 7 are also members of set 𝐵, these elements are only listed one time. Lastly, set 𝐵 includes the unique element 2, so 2 is also included as part of the union of sets 𝐴 and 𝐵.
TRY IT 4
Set 𝐴={2, 4, 5, 8} and set 𝐵={3, 4, 7}. Find 𝐴 union 𝐵.
Show / Hide Solution
{2, 3, 4, 5, 7, 8}
When observing the union of sets 𝐴 and 𝐵, notice that both set 𝐴 and set 𝐵 are subsets of 𝐴 union 𝐵. Graphically, 𝐴 union 𝐵 can be represented in several different ways depending on the members that they have in common. If 𝐴 and 𝐵 are disjoint sets, then 𝐴 union 𝐵 would be represented with two disjoint circles within the universal set, as shown in the Venn diagram below.
If sets 𝐴 and 𝐵 share some, but not all, members in common, then the Venn diagram is drawn as two separate circles that overlap.
If every member of set 𝐴 is also a member of set 𝐵, then 𝐴 is a subset of set 𝐵, and 𝐴 union 𝐵 would be equal to set 𝐵. To draw the Venn diagram, the circle representing set 𝐴 should be completely enclosed in the circle containing set 𝐵.
EXAMPLE 5
Set 𝐴={0,2,4,6,8} and set 𝐵={1,3,5,7,9}. Find 𝐴∪𝐵.
Show / Hide Solution
Because sets 𝐴 and 𝐵 are disjoint, the union is simply the set containing all the elements in both set 𝐴 and set 𝐵. 𝐴∪𝐵={0,1,2,3,4,5,6,7,8,9}.
TRY IT 5
Set 𝐴={2, 3, 5} and set 𝐵={4, 6, 8}. Find 𝐴∪𝐵.
Show / Hide Solution
{2, 3, 4, 5, 6, 8}
EXAMPLE 6
Set 𝐴={1,3,5,…} and set 𝐵=ℕ={1,2,3,…}. Find 𝐴∪𝐵.
Show / Hide Solution
Because set 𝐴 is a subset of set 𝐵, 𝐴 union 𝐵 is equal to set 𝐵. 𝐴∪𝐵=ℕ={1,2,3,…}=𝐵.
TRY IT 6
Set 𝐴={𝑎,𝑏,𝑐,…,𝑧} and set 𝐵={𝑎,𝑒,𝑖,𝑜,𝑢}. Find 𝐴∪𝐵.
Show / Hide Solution
{ a, b, c, …,z}
Determining the Cardinality of Two Sets
The cardinality of the union of two sets is the total number of elements in the set. Symbolically the cardinality of 𝐴 union 𝐵 is written, 𝑛(𝐴∪𝐵). If two sets 𝐴 and 𝐵 are disjoint, the cardinality of 𝐴 union 𝐵 is the sum of the cardinality of set 𝐴 and the cardinality of set 𝐵. If the two sets intersect, then 𝐴 intersection 𝐵 is a subset of both set 𝐴 and set 𝐵. This means that if we add the cardinality of set 𝐴 and set 𝐵, we will have added the number of elements in 𝐴 intersection 𝐵 twice, so we must then subtract it once as shown in the formula that follows.
The cardinality of 𝐴 union 𝐵 is found by adding the number of elements in set 𝐴 to the number of elements in set 𝐵, then subtracting the number of elements in the intersection of set 𝐴 and set 𝐵.
𝑛(𝐴∪𝐵)=𝑛(𝐴)+𝑛(𝐵)−𝑛(𝐴∩𝐵),
n(A∪B)=n(A)+n(B)−n(A∩B), or 𝑛(𝐴or𝐵)=𝑛(𝐴)+𝑛(𝐵)−𝑛(𝐴and𝐵).
If sets 𝐴 and 𝐵 are disjoint, then 𝑛(𝐴∩𝐵)=𝑛(𝐴and𝐵)=0 and the formula is still valid, but simplifies to 𝑛(𝐴∪𝐵)=𝑛(𝐴)+𝑛(𝐵).
EXAMPLE 7
The number of elements in set 𝐴 is 10, the number of elements in set 𝐵 is 20, and the number of elements in 𝐴 intersection 𝐵 is 4. Find the number of elements in 𝐴 union 𝐵.
Show / Hide Solution
Using the formula for determining the cardinality of the union of two sets, we can say 𝑛(𝐴∪𝐵)=𝑛(𝐴)+𝑛(𝐵)−𝑛(𝐴∩𝐵)=10+20−4=26.
TRY IT 7
If 𝑛(𝐴)=23,𝑛(𝐵)=17, and 𝑛(𝐴∩𝐵)=7,then find 𝑛(𝐴∪𝐵).
Show / Hide Solution
33
EXAMPLE 8
If 𝐴 and 𝐵 are disjoint sets and the cardinality of set 𝐴 is 37 and the cardinality of set 𝐵 is 43, find the cardinality of 𝐴 union 𝐵.
Show / Hide Solution
To find the cardinality of 𝐴 union 𝐵, apply the formula, 𝑛(𝐴∪𝐵)=𝑛(𝐴)+𝑛(𝐵)−𝑛(𝐴∩𝐵). Because sets 𝐴 and 𝐵 are disjoint, 𝐴∩𝐵 is the empty set, therefore 𝑛(𝐴∩𝐵)=𝑛(∅)=0 and 𝑛(𝐴∪𝐵)=37+43−0=80.
TRY IT 8
If 𝐴∩𝐵=∅,𝑛(𝐴)=35, and 𝑛(𝐵)=78, then find 𝑛(𝐴∪𝐵).
Show / Hide Solution
113
Applying Concepts of “AND” and “OR” to Set Operations
To become a licensed driver, you must pass some form of written test and a road test, along with several other requirements depending on your age. To keep this example simple, let us focus on the road test and the written test. If you pass the written test but fail the road test, you will not receive your license. If you fail the written test, you will not be allowed to take the road test and you will not receive a license to drive. To receive a driver’s license, you must pass the written test AND the road test. For an “AND” statement to be true, both conditions that make up the statement must be true. Similarly, the intersection of two sets A and B is the set of elements that are in both set 𝐴 and set 𝐵. To be a member of 𝐴 intersection 𝐵, an element must be in set 𝐴 and also must be in set 𝐵. The intersection of two sets corresponds to a logical “AND” statement.
The union of two sets is a logical inclusive “OR” statement. Say you are at a birthday party and the host offers Leah, Lenny, Maya, and you some cake or ice cream for dessert. Leah asks for cake, Lenny accepts both cake and ice cream, Maya turns down both, and you choose only ice cream. Leah, Lenny, and you are all having dessert. The “OR” statement is true if at least one of the components is true. Maya is the only one who did not have cake or ice cream; therefore, she did not have dessert and the “OR” statement is false. To be in the union of two sets 𝐴 and 𝐵, an element must be in set 𝐴 or set 𝐵 or both set 𝐴 and set 𝐵.
EXAMPLE 9
𝐴={0,3,6,9,12}, 𝐵={0,4,8,12,16}, and 𝐶={1,2,3,5,8,13}.
Find the set consisting of elements in:
- 𝐴 and 𝐵.
- 𝐴 or 𝐵.
- 𝐴 or 𝐶.
- (𝐵 and 𝐶) or 𝐴.
Show / Hide Solution
- 𝐴and𝐵=𝐴∩𝐵={0,12}, because only the elements 0 and 12 are members of both set 𝐴 and set 𝐵.
- 𝐴or𝐵=𝐴∪𝐵={0,3,4,6,8,9,12,16}, because the set 𝐴 or 𝐵 is the collection of all elements in set 𝐴 or set 𝐵, or both.
- 𝐴or𝐶=𝐴∪𝐶={0,1,2,3,5,6,8,9,12,13}, because the set 𝐴 or 𝐶 is the collection of all elements in set 𝐴 or set 𝐶, or both.
- (𝐵and𝐶)or𝐴=(𝐵∩𝐶)∪𝐴. Parentheses are evaluated first: (𝐵and𝐶)=𝐵∩𝐶={8}, because the only member that both set 𝐵 and set 𝐶 share in common is 8. So, now we need to find {8}or{0,3,6,9,12}, because the word translates to the union operation, the problem becomes {8}∪{0,3,6,9,12}, which is equal to {0,3,6,8,9,12}.
TRY IT 9
𝐴= {m, a, t, h}, and 𝐵= {i, s}, and 𝐶= {e, a, s, y}. Find the set consisting of elements in:
- 𝐴 or 𝐵.
- 𝐴 and 𝐶.
- 𝐵 or 𝐶.
- (𝐴 and 𝐶) and 𝐵.
Show / Hide Solution
- {m, a, t, h, i, s}
- {a}
- {i, s, e, a, y}
- {}
EXAMPLE 10
Geordie Stenner is serving cake and ice cream at his Canada Day celebration party. The party has a total of 54 guests in attendance. Suppose 30 guests requested cake, 20 guests asked for ice cream, and 12 guests did not have either cake or ice cream.
- How many guests had cake or ice cream?
- How many guests had cake and ice cream?
Show / Hide Solution
- The total number of people at the party is 54, and 12 people did not have cake or ice cream. Recall that the total number of elements in the universal set is always equal to the number of elements in a subset plus the number of elements in the complement of the set, 𝑛(𝑈)=𝑛(𝐴)+𝑛(𝐴′). That means 54=𝑛(cake or ice cream)+𝑛(not(cake or ice cream)), or equivalently, 𝑛(cake∪ice cream)=54−𝑛((cake∪ice cream)′)=54−12=42. A total of 42 people at the party had cake or ice cream.
- To determine the number of people who had both cake and ice cream, we need to find the intersection of the set of people who had cake and the set of people who had ice cream. From Question 1, the number of people who had cake or ice cream is 42. This is the union of the two sets. The formula for the union of two sets is 𝑛(𝐴∪𝐵)=𝑛(𝐴)+𝑛(𝐵)−𝑛(𝐴∩𝐵). Use the information given in the problem and substitute the known values into the formula to solve for the number of people in the intersection: 42=30+20−𝑛(𝐴∩𝐵). Adding 30 and 20, the equation simplifies to 42=50−𝑛(cake and ice cream). Which means 𝑛(cake and ice cream)=50−42=8.
TRY IT 10
- How many guests had soup or salad or both?
- How many guests had both soup and a salad?
Show / Hide Solution
- 127
- 50
Who knew?
The Real Inventor of the Venn Diagram
John Venn, in his writings, references works by both John Boole and Augustus De Morgan, who referred to the circle diagrams commonly used to present logical relationships as Euler’s circles. Leonhard Euler’s works were published over 100 years prior to Venn’s, and Euler may have been influenced by the works of Gottfried Leibniz.
So, why does John Venn get all the credit for these graphical depictions? Venn was the first to formalize the use of these diagrams in his book Symbolic Logic, published in 1881. Further, he made significant improvements in their design, including shading to highlight the region of interest. The mathematician C.L. Dodgson, also known as Lewis Carroll, built upon Venn’s work by adding an enclosing universal set.
Invention is not necessarily coming up with an initial idea. It is about seeing the potential of an idea and applying it to a new situation.
References:
Margaret E. Baron. “A Note on the Historical Development of Logic Diagrams: Leibniz, Euler and Venn.” The Mathematical Gazette, vol. 53, no. 384, 1969, pp. 113-125. JSTOR, www.jstor.org/stable/3614533. Accessed 15 July 2021.
Deborah Bennett. “Drawing Logical Conclusions.” Math Horizons, vol. 22, no. 3, 2015, pp. 12-15. JSTOR, www.jstor.org/stable/10.4169/mathhorizons.22.3.12. Accessed 15 July 2021.
Drawing Conclusions from a Venn Diagram with Two Sets
All Venn diagrams will display the relationships between the sets, such as subset, intersecting, and/or disjoint. In addition to displaying the relationship between the two sets, there are two main additional details that Venn diagrams can include: the individual members of the sets or the cardinality of each disjoint subset of the universal set.
A Venn diagram with two subsets will partition the universal set into 3 or 4 sections depending on whether they are disjoint or intersecting sets. Recall that the complement of set 𝐴, written 𝐴′, is the set of all elements in the universal set that are not in set 𝐴
EXAMPLE 11
- Find 𝐴∪𝐵.
- Find 𝐴∩𝐵.
- Find 𝐵′.
- Find 𝑛(𝐵′).
Show / Hide Solution
- 𝐴∪𝐵= {1,2,3,4,5,6,7,8}, because 𝐴 union 𝐵 is the collection of all elements in set 𝐴 or set 𝐵 or both.
- Because 𝐴 and 𝐵 are disjoint sets, there are no elements that are in both 𝐴 and 𝐵. Therefore, 𝐴 intersection 𝐵 is the empty set, 𝐴∩𝐵=∅.
- The complement of set 𝐵 is the set of all elements in the universal set that are not in set 𝐵: 𝐵′= {0,1,3,5,7,9}.
- The cardinality, or number of elements in set 𝐵′, is 𝑛(𝐵′) =6.
TRY IT 11
- Find 𝐴∩𝐵.
- Find 𝐴∪𝐵.
- Find 𝐴∩𝐵.
- Find 𝑛(𝐴∩𝐵′).
Show / Hide Solution
- {3, 5, 7}
- {1, 2, 3, 5, 7,9}
- [1, 9}
- 2
EXAMPLE 12
Using a Venn Diagram to Draw Conclusions about Set Cardinality
- Find
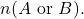
- Find
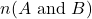 .
. - Find
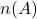 .
.
Show / Hide Solution
- The number of elements in 𝐴 or 𝐵 is the number of elements in 𝐴 union 𝐵: 𝑛(𝐴∪𝐵) = 𝑛 ({2,5,7}) =14.
- The number of elements in 𝐴 and 𝐵 is the number of elements in 𝐴 intersection 𝐵: 𝑛(𝐴∩𝐵) =5.
- The number of elements in set 𝐴 is the sum of all the numbers enclosed in the circle representing set 𝐴: 𝑛(𝐴)=𝑛 ({7,5}) =12.
TRY IT 12
- Find
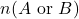 .
. - Find
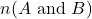 .
. - Find
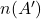 .
.
Show / Hide Solution
- 40
- 0
- 27
Check your understanding
- The ___________ of two sets
 and
and 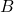 is the set of all elements that they share in common.
is the set of all elements that they share in common. - The ___________ of two sets
 and
and 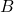 is the collection of all elements that are in set
is the collection of all elements that are in set  or set
or set  , or both set
, or both set  and set
and set  .
. - The union of two sets
 and
and  is represented symbolically as __________.
is represented symbolically as __________. - The intersection of two sets
 and
and  is represented symbolically as ___________.
is represented symbolically as ___________. - If set
 is a subset of set
is a subset of set 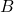 , then
, then  intersection
intersection 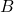 is equal to set ___________.
is equal to set ___________. - If set
 is a subset of set
is a subset of set 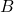 , then
, then  union
union 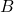 is equal to set ___________.
is equal to set ___________. - If set
 and set
and set 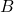 are disjoint sets, then
are disjoint sets, then  intersection
intersection 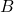 is the ___________ set.
is the ___________ set. - The cardinality of
 union
union 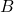 ,
, 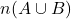 is found using the formula: ___________.
is found using the formula: ___________.
Check your understanding answers
- intersection
- union
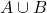

- A
- B
- empty
1.4 Exercise Set
For the following exercises, determine the union or intersection of the sets as indicated. ![]() ,
, ![]() ,
, ![]() , and
, and ![]() .
.
For the following exercises, use the sets provided to apply the “AND” or “OR” operation as indicated to find the resulting set. ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() .
.
- Find the set consisting of elements in
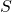 and
and 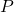 .
. - Find the set consisting of elements in
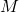 or
or 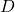 .
. - Find the set consisting of elements in
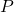 or
or 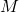 .
. - Find the set consisting of elements in
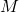 and
and 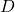 .
. - Find the set consisting of elements in
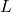 and
and 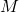 .
. - Find the set consisting of elements in
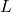 or
or 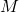 .
. - Find the set consisting of the elements in
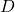 or
or 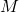 or
or 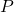 .
. - Find the set consisting of the elements in
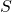 or
or 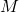 or
or 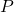 .
. - Find the set consisting of the elements in (
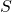 or
or 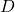 ) and
) and 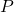 .
. - Find the set consisting of the elements in
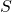 or (
or (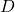 and
and 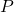 ).
). - Find the set consisting of elements in
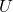 or (
or (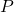 and
and 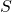 ).
). - Find the set consisting of elements in (
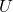 or
or 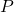 ) and
) and 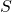 .
.
For the following exercises, use the Venn diagram provided to answer the following questions about the sets.
- Find
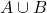 .
. - Find
 .
. - Find
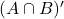 .
. - Find
 .
. - Find
 .
. - Find
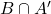 .
.
For the following exercises, use the Venn diagram provided to answer the following questions about the sets.
- Find
 .
. - Find
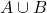 .
. - Find
 .
. - Find
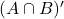 .
. - Find
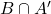 .
. - Find
 .
.
For the following exercises, use the Venn diagram provided极 to answer the following questions about the sets.
- Find
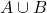 .
. - Find
 .
. - Find
 .
. - Find
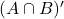 .
. - Find
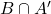 .
. - Find
 .
.
For the following exercises, determine the cardinality of the union of set ![]() and set
and set ![]() .
.
- If set
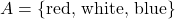 and set
and set 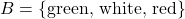 , find
, find 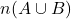 .
. - If set
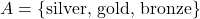 and set
and set 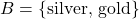 , find the number of elements in
, find the number of elements in  or
or 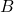 .
. - If set
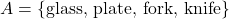 and set
and set 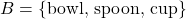 , find the number of elements in
, find the number of elements in  or
or 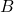 .
. - If set
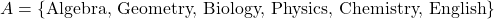 and Set
and Set 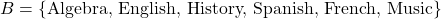 , find
, find 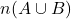 .
.
For the following exercises, use the Venn diagram to determine the cardinality of ![]() union
union ![]() .
.
Show / Hide Solution
- 40
- 0
- 27
Attribution
Text Attribution
This text was adapted from Chapter 1.4 of Contemporary Mathematics, textbooks originally published by OpenStax.
