3.3 What Are the Odds?
Learning Objectives
After completing this section, you should be able to:
- Compute odds.
- Determine odds from probabilities.
- Determine probabilities from odds.
A particular lottery instant-win game has 2 million tickets available. Of those, 500,000 win a prize. If there are 500,000 winners, then it follows that there are 1,500,000 losing tickets. When we evaluate the risk associated with a game like this, it can be useful to compare the number of ways to win the game to the number of ways to lose. In the case of this game, we would compare the 500,000 wins to the 1,500,000 losses. In other words, there are 3 losing tickets for every winning ticket. Comparisons of this type are the focus of this section.
Computing Odds
The ratio of the number of equally likely outcomes in an event ![]() to the number of equally likely outcomes not in the event
to the number of equally likely outcomes not in the event ![]() is called the odds for (or odds in favor of) the event. The opposite ratio (the number of outcomes not in the event to the number in the event
is called the odds for (or odds in favor of) the event. The opposite ratio (the number of outcomes not in the event to the number in the event ![]() to the number in the event
to the number in the event ![]() is called the odds against the event.
is called the odds against the event.
Checkpoint
Both odds and probabilities are calculated as ratios. To avoid confusion, we will always use fractions, decimals, or percents for probabilities, and we’ll use colons to indicate odds. The rules for simplifying fractions apply to odds, too. Thus, the odds for winning a prize in the game described in the section opener are ![]() and the odds against winning a prize are
and the odds against winning a prize are ![]() . These would often be described in words as “the odds of winning are one to three in favor” or “the odds of winning are three to one against.”
. These would often be described in words as “the odds of winning are one to three in favor” or “the odds of winning are three to one against.”
Checkpoint
Notice that, while probabilities must always be between zero and one inclusive, odds can be any (non-negative) number, as we’ll see in the next example.
Example 1
- If you roll a fair 6-sided die, what are the odds for rolling a 5 or higher?
- If you roll two fair 6-sided dice, what are the odds against rolling a sum of 7?
- If you draw a card at random from a standard deck, what are the odds for drawing a ♡?
- If you draw 2 cards at random from a standard deck, what are the odds against them both being ♠?
Show/Hide Solution
- The sample space for this experiment is {1, 2, 3, 4, 5, 6}. Two of those outcomes are in the event “roll a five or higher,” while four are not. So, the odds for rolling a five or higher are
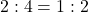 .
. - In Example 7.18, we found the sample space for this experiment using the following table (Figure 7.34):
Figure 7.34 There are 6 outcomes in the event “roll a sum of 7,” and there are 30 outcomes not in the event. So, the odds against rolling a 7 are
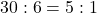 .
. - There are 13 ♡ in a standard deck, and
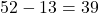 others. So, the odds in favor of drawing a ♡ are
others. So, the odds in favor of drawing a ♡ are 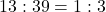 .
. - There are
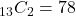 ways to draw 2 ♠, and
ways to draw 2 ♠, and 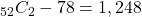 ways to draw 2 cards that are not both ♠. So, the odds against drawing 2 ♠ are
ways to draw 2 cards that are not both ♠. So, the odds against drawing 2 ♠ are 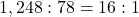 .
.
Try It 1
You roll a pair of 4-sided dice with faces labeled 1 through 4.
- What are the odds for rolling a sum greater than 3?
- What are the odds against both dice giving the same number?
Show Solution
1. The sample space:
| Sums | 2nd roll | ||||
| 1st roll | Choices | 1 | 2 | 3 | 4 |
| 1 | 2 | 3 | 4 | 5 | |
| 2 | 3 | 4 | 5 | 6 | |
| 3 | 4 | 5 | 6 | 7 | |
| 4 | 5 | 6 | 7 | 8 |
The total number of outcomes: 16.
The outcomes greater than three: 13.
The number of outcomes not in the desired event is ![]() .
.
The ratio of the number of equally likely outcomes in an event ![]() to the number of equally likely outcomes not in the event is called the odds for (or odds in favor of) the event.
to the number of equally likely outcomes not in the event is called the odds for (or odds in favor of) the event.
The odds in favor of your event are 13: 3.
2. The sample space:
| Both Rolls | 2nd roll | ||||
| 1st roll | Choices | 1 | 2 | 3 | 4 |
| 1 | 1,1 | 1,2 | 1,3 | 1,4 | |
| 2 | 2,1 | 2.2 | 2,3 | 2,4 | |
| 3 | 3,1 | 3,2 | 3,3 | 3,4 | |
| 4 | 4,1 | 4,2 | 4,3 | 4,4 |
The total number of outcomes: 16.
The outcomes with both dice giving the same number: 4.
The number of outcomes not in the desired event is ![]() .
.
The ratio of the number of equally likely outcomes in an event ![]() to the number of equally likely outcomes not in the event is called the odds for (or odds in favor of) the event.
to the number of equally likely outcomes not in the event is called the odds for (or odds in favor of) the event.
The odds against your event are 12:4 or 3:1.
Odds as a Ratio of Probabilities
We can also think of odds as a ratio of probabilities. Consider again the instant-win game from the section opener, with 500,000 winning tickets out of 2,000,000 total tickets. If a player buys one ticket, the probability of winning is ![]() , and the probability of losing is
, and the probability of losing is ![]() . Notice that the ratio of the probability of winning to the probability of losing is
. Notice that the ratio of the probability of winning to the probability of losing is ![]() , which matches the odds in favor of winning.
, which matches the odds in favor of winning.
For an event ![]() ,
,
![]()
We can use these formulas to convert probabilities to odds, and vice versa.
EXAMPLE 3
Given the following probabilities of an event, find the corresponding odds for and odds against that event.
Show/Hide Solution
- Using the formula, we have:
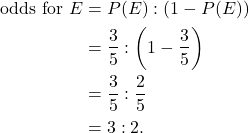
(Note that in the last step, we simplified by multiplying both terms in the ratio by 5.)
Since the odds for are
are 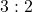 , the odds against
, the odds against  must be
must be 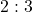 .
. - Again, we’ll use the formula:
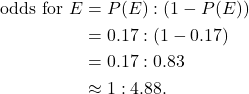
(In the last step, we simplified by dividing both terms in the ratio by 0.17.)
It follows that the odds against are approximately
are approximately 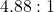 .
.
TRY IT 3
If the probability of an event ![]() is 80%, find the odds for and the odds against
is 80%, find the odds for and the odds against ![]() .
.
Show Solution
Odds for:If the probability is 80%, then the odds for the event are ![]() .
.
![]()
You can simplify the ratio by dividing both numbers by 0.8.
![]()
You can multiply again by 4 to get rid of decimals.
![]()
Odds against: (reverse the numbers).
![]()
The odds for E are 4:1 and the odds against E are 1:4.
Now, let’s convert odds to probabilities. Let’s say the odds for an event are ![]() . Then, using the formula above, we have
. Then, using the formula above, we have ![]() . Converting to fractions and solving for
. Converting to fractions and solving for ![]() , we get:
, we get:
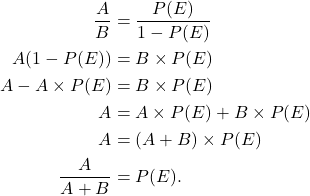
Let’s put this result in a formula we can use.
If the odds in favor of ![]() are
are ![]() , then
, then
![]()
EXAMPLE 4
Find ![]() if
if ![]() :
:
- The odds of
 are
are 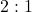 in favor
in favor - The odds of
 are
are 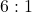 against
against
Show/Hide Solution
- Using the formula we just found, we have
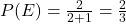 .
. - If the odds against are
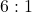 , then the odds for are
, then the odds for are 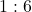 . Thus, using the formula,
. Thus, using the formula, 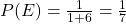 .
.
TRY IT 4
Find ![]() if
if ![]() :
:
- The odds of
 are
are 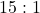 against
against - The odds of
 are
are 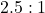 in favor
in favor
Show Solution
1. The odds in favor of ![]() are 1: 15.If the odds in favor of
are 1: 15.If the odds in favor of ![]() are
are ![]() , then
, then ![]() .
.
![]()
2. The odds in favor of ![]() are
are ![]() .
.
If the odds in favor of ![]() are
are ![]() , then
, then ![]() .
.
![]()
Checkpoint
Some places, particularly state lottery websites, will use the words “odds” and “probability” interchangeably. Never assume that the word “odds” is being used correctly! Compute one of the odds/probabilities yourself to make sure you know how the word is being used!
Check your understanding
For the following exercises, you are rolling a 6-sided die with 3 orange faces, 2 green faces, and 1 blue face.
- What are the odds in favor of rolling a green face?
- What are the odds against rolling a blue face?
- What are the odds in favor of rolling an orange face?
- What are the odds in favor of an event with probability
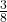 ?
? - What are the odds against an event with probability
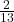 ?
? - What is the probability of an event with odds
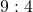 against?
against? - What is the probability of an event with odds
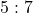 in favor?
in favor?
Check your understanding answers
- The total number of outcomes: 6. The outcomes with a green face: 2. The number of outcomes not in the desired event is
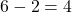 . The odds in favor of rolling a green face are
. The odds in favor of rolling a green face are 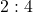 or
or 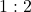 .
. - The total number of outcomes is 6. The number of outcomes with a blue face is 1. The number of outcomes not in the desired event is
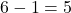 . The odds against rolling a blue face are
. The odds against rolling a blue face are 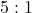 .
. - The total number of outcomes is 6. The number of outcomes with an orange face is 3. The number of outcomes not in the desired event is
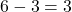 . The odds in favor of rolling an orange face is
. The odds in favor of rolling an orange face is 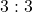 or
or 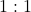 .
. - Odds for: If the probability is
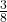 then the odds for the event are
then the odds for the event are 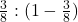 .
.  Multiply both numbers by 8 to clear fractions. 3:5
Multiply both numbers by 8 to clear fractions. 3:5 - Odds for: If the probability is
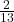 then the odds for the event are
then the odds for the event are 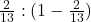 .
. 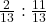 Multiply both numbers by 13 to clear fractions. 2:11 Reverse the ratio to find the odds against the event.11: 2
Multiply both numbers by 13 to clear fractions. 2:11 Reverse the ratio to find the odds against the event.11: 2 - The odds in favor of
 are 4:9. If the odds in favor of
are 4:9. If the odds in favor of  are
are 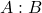 , then
, then 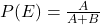 .
. 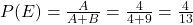
- The odds in favor of
 are 5:7. If the odds in favor of
are 5:7. If the odds in favor of  are
are 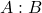 , then
, then 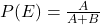 .
. 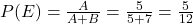
3.4 Exercise Set
For the following exercises, find the probabilities of events with the given odds in favor.
For the following exercises, find the probabilities of events with the given odds against.
In the following exercises, find the odds in favor of events with the given probabilities. Give your answer as a ratio of whole numbers. If neither of those two numbers is 1, also give an answer as a ratio involving both 1 and a number greater than or equal to 1 (for example, the odds ![]() and
and ![]() can be reduced to
can be reduced to ![]() and
and ![]() ).
).
In the following exercises, find the odds against events with the given probabilities. Give your answer as a ratio of whole numbers. If neither of those two numbers is 1, also give an answer as a ratio involving both 1 and a number greater than or equal to 1 (for example, the odds ![]() and
and ![]() can be reduced to
can be reduced to ![]() and
and ![]() ).
).
In the following exercises, you are drawing from a deck containing only these 10 cards: A♡, A♠, A♣, A♢, K♠, K♣, Q♡, Q♠, J♡, J♠.
- Let
 be the event “draw an ace.”
be the event “draw an ace.”
- What is the probability of
 ?
? - What are the odds in favor of
 ?
? - What are the odds against
 ?
?
- What is the probability of
- Let
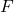 be the event “draw a ♡”.
be the event “draw a ♡”.
- What is the probability of
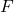 ?
? - What are the odds in favor of
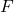 ?
? - What are the odds against
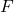 ?
?
- What is the probability of
- Let
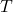 be the event “draw two ♠ (without replacement).”
be the event “draw two ♠ (without replacement).”
- What is the probability of
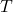 ?
? - What are the odds in favor of
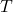 ?
? - What are the odds against
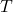 ?
?
- What is the probability of
Text Attribution
This text was adapted from Chapter 7.7 of Contemporary Mathematics, textbooks originally published by OpenStax.
