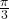Answer Key Chapter 7 – Algebra and Trigonometry 2e | OpenStax
7.1 Angles
-
Figure 1 Graph of a 240-degree angle with a counterclockwise rotation. 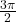
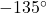
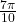
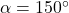
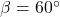
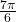
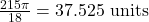
- 1.88
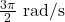
- 1655 kilometers per hour
7.2 Right Triangle Trigonometry
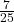
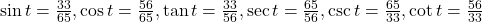
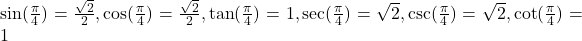
- 2
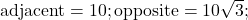 missing angle is
missing angle is 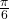
- About 52 ft
7.3 Unit Circle
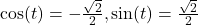
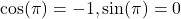
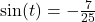
- approximately 0.866025403
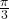
- a.
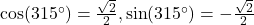 b.
b. 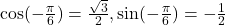
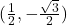
7.4 The Other Trigonometric Functions
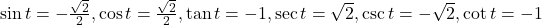
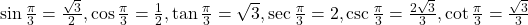
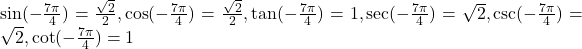
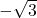
- -2
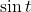
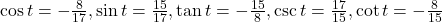
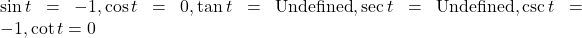
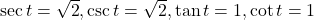
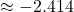
7.1 Section Exercises
-
Figure 1 Graph of a circle with an angle inscribed, showing the initial side, terminal side, and vertex. - Whether the angle is positive or negative determines the direction. A positive angle is drawn in the counterclockwise direction, and a negative angle is drawn in the clockwise direction.
- Linear speed is a measurement found by calculating distance of an arc compared to time. Angular speed is a measurement found by calculating the angle of an arc compared to time.
-
Figure 4 Graph of a circle with an angle inscribed. -
Figure 5 Graph of a circle with a 135 degree angle inscribed. -
Figure 6 Graph of a circle with a 2pi/3 radians angle inscribed. -
Figure 7 Graph of a circle with 5pi/6 radians angle inscribed. -
Figure 8 Graph of a circle with a –pi/10 radians angle inscribed. 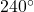
Figure 9 Graph of a circle showing the equivalence of two angles. 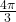
Figure 10 Graph of a circle showing the equivalence of two angles. 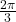
Figure 11 Graph of a circle showing the equivalence of two angles. 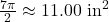
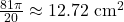
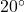
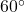
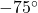
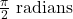
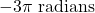
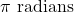
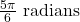
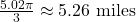
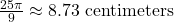
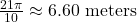
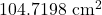
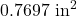
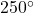
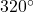
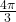
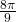
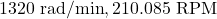
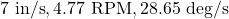
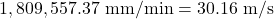
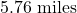
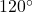
- 794 miles per hour
- 2,234 miles per hour
- 11.5 inches
7.2 Section Exercises
-
Figure 12 A right triangle with side opposite, adjacent, and hypotenuse labeled. - The tangent of an angle is the ratio of the opposite side to the adjacent side.
- For example, the sine of an angle is equal to the cosine of its complement; the cosine of an angle is equal to the sine of its complement.
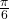
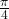
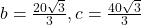
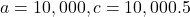

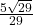
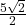
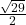
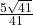
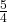
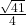
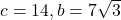
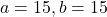
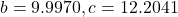
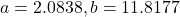
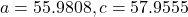
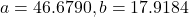
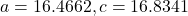
- 188.3159
- 200.6737
- 498.3471 ft
- 1060.09 ft
- 27.372 ft
- 22.6506 ft
- 368.7633 ft
7.3 Section Exercises
- The unit circle is a circle of radius 1 centered at the origin.
- Coterminal angles are angles that share the same terminal side. A reference angle is the size of the smallest acute angle, t, formed by the terminal side of the angle t and the horizontal axis.
- The sine values are equal.
- I
- IV
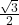
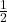
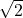
- 0
- -1
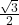
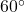
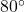
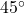
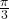
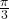
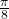
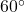 , Quadrant IV,
, Quadrant IV, 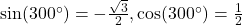
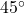 , Quadrant II,
, Quadrant II, 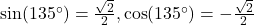
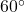 , Quadrant II,
, Quadrant II, 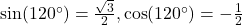
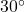 , Quadrant II,
, Quadrant II, 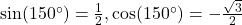
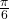 , Quadrant III,
, Quadrant III, 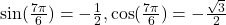
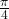 , Quadrant II,
, Quadrant II, 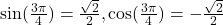
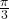 , Quadrant II,
, Quadrant II, 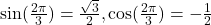
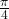 , Quadrant IV,
, Quadrant IV, 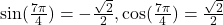
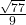
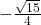
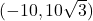
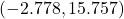
![Rendered by QuickLaTeX.com [-1, 1]](https://foundations-of-math12.pressbooks.tru.ca/wp-content/ql-cache/quicklatex.com-b540568b7d209448fcf74b9e61ebac4d_l3.png)
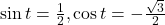
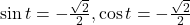
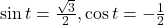
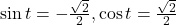
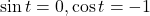
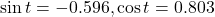
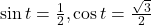
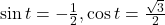
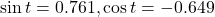
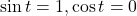
- -0.1736
- 0.9511
- -0.7071
- -0.1392
- -0.7660
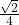
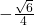
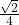
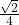
- 0
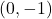
- 37.5 seconds, 97.5 seconds, 157.5 seconds, 217.5 seconds, 277.5 seconds, 337.5 seconds
7.4 Section Exercises
- Yes, when the reference angle is
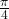 and the terminal side of the angle is in quadrants I and III. Thus, at
and the terminal side of the angle is in quadrants I and III. Thus, at 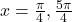 , the sine and cosine values are equal.
, the sine and cosine values are equal. - Substitute the sine of the angle in for y in the Pythagorean Theorem
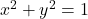 . Solve for x and take the negative solution.
. Solve for x and take the negative solution. - The outputs of tangent and cotangent will repeat every
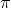 units.
units. 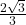
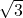
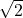
- 1
- 2
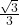
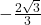
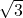
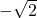
- –1
- -2
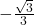
- 2
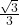
- –2
- –1
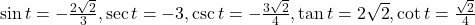
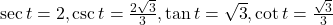
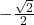
- 3.1
- 1.4
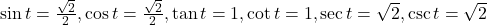
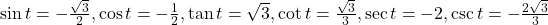
- –0.228
- –2.414
- 1.414
- 1.540
- 1.556
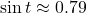
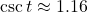
- even
- even
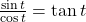
- 13.77 hours, period:
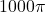
- 3.46 inches
Review Exercises
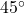
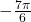
- 10.385 meters
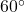
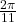
-
Figure 13 This is an image of a graph of a circle with a negative angle inscribed. -
Figure 14 This is an image of a graph of a circle with an angle inscribed. - 1036.73 miles per hour
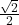
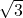
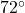
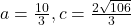
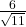
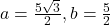
- 369.2136 ft
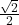
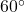
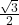
- all real numbers
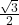
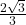
- 2
- –2.5
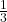
- cosine, secant
Practice Test
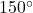
- 6.283 centimeters
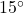
-
Figure 15 This is an image of a graph of a circle with an angle inscribed. - 3.351 feet per second,
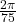 radians per second
radians per second 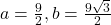
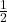
- real numbers
- 1
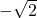
- –0.68