Answer Key Chapter 8 – Algebra and Trigonometry 2e | OpenStax

imazur

Answer Key Chapter 8 – Algebra and Trigonometry 2e | OpenStax

Try It

8.1 Graphs of the Sine and Cosine Functions

1. $6\pi$

2. $\frac{1}{2}$ compressed

3. $\frac{\pi}{2}$ ; right

4. 2 units up

5. midline: $y=0$ ; amplitude: $| A |=\frac{1}{2}$ ; period: $P=\frac{2\pi}{| B |}=6\pi$ ; phase shift: $\frac{C}{B}=\pi$

6. $f(x)=\sin(x)+2$

7. two possibilities: $y=4\sin(\frac{\pi}{5}x-\frac{\pi}{5})+4$ or $y=-4\sin(\frac{\pi}{5}x+\frac{4\pi}{5})+4$

8.

A graph of -0.8cos(2x). Graph has range of [-0.8, 0.8], period of pi, amplitude of 0.8, and is reflected about the x-axis compared to it's parent function cos(x). — A graph of -0.8cos(2x). Graph has range of [-0.8, 0.8], period of pi, amplitude of 0.8, and is reflected about the x-axis compared to it’s parent function cos(x).

midline: $y=0$ ; amplitude: $| A |=0.8$ ; period: $P=\frac{2\pi}{| B |}=\pi$ ; phase shift: $\frac{C}{B}=0$ or none

9.

A graph of -2cos((pi/3)x+(pi/6)). Graph has amplitude of 2, period of 6, and has a phase shift of 0.5 to the left.

midline: $y=0$ ; amplitude: $| A |=2$ ; period: $P=\frac{2\pi}{| B |}=6$ ; phase shift: $\frac{C}{B}=-\frac{1}{2}$

10. 7

A graph of 7cos(x). Graph has amplitude of 7, period of 2pi, and range of [-7,7].

11. $y=3\cos(x)-4$

A cosine graph with range [-1,-7]. Period is 2 pi. Local maximums at (0,-1), (2pi,-1), and (4pi, -1). Local minimums at (pi,-7) and (3pi, -7).

8.2 Graphs of the Other Trigonometric Functions

1.

A graph of two periods of a modified tangent function, with asymptotes at x=-3 and x=3.

2. It would be reflected across the line $y=-1$ , becoming an increasing function.

3. $g(x)=4\tan(2x)$

4. This is a vertical reflection of the preceding graph because $A$ is negative.

A graph of one period of a modified secant function, which looks like an downward facing prarbola and a upward facing parabola.

5.

A graph of one period of a modified secant function. There are two vertical asymptotes, one at approximately x=-pi/20 and one approximately at 3pi/16.

6.

7.

A graph of two periods of both a secant and consine function. Grpah shows that cosine function has local maximums where secant function has local minimums and vice versa.

8.3 Inverse Trigonometric Functions

1. $\arccos(0.8776)\approx 0.5$

2.

$-\frac{\pi}{2}$ ;
$-\frac{\pi}{4}$ ;
$\pi$ ;
$\frac{\pi}{3}$

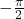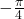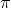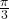
3. 1.9823 or 113.578°

4. $\sin^{-1}(0.6)=36.87^{\circ}=0.6435$ radians

5. $\frac{\pi}{8}; \frac{2\pi}{9}$

6. $\frac{3\pi}{4}$

7. $\frac{12}{13}$

8. $\frac{4\sqrt{2}}{9}$

9. $\frac{4x}{\sqrt{16x^2+1}}$

8.1 Section Exercises

1. The sine and cosine functions have the property that $f(x+P)=f(x)$ for a certain $P$ . This means that the function values repeat for every $P$ units on the x-axis.

3. The absolute value of the constant $A$ (amplitude) increases the total range and the constant $D$ (vertical shift) shifts the graph vertically.

5. At the point where the terminal side of $t$ intersects the unit circle, you can determine that the $\sin t$ equals the y-coordinate of the point.

7.

A graph of (2/3)cos(x). Graph has amplitude of 2/3, period of 2pi, and range of [-2/3, 2/3].

amplitude: $\frac{2}{3}$ ; period: $2\pi$ ; midline: $y=0$ ; maximum: $y=\frac{2}{3}$ occurs at $x=0$ ; minimum: $y=-\frac{2}{3}$ occurs at $x=\pi$ ; for one period, the graph starts at 0 and ends at $2\pi$

9.

A graph of 4sin(x). Graph has amplitude of 4, period of 2pi, and range of [-4, 4].

amplitude: 4; period: $2\pi$ ; midline: $y=0$ ; maximum $y=4$ occurs at $x=\frac{\pi}{2}$ ; minimum: $y=-4$ occurs at $x=\frac{3\pi}{2}$ ; one full period occurs from $x=0$ to $x=2\pi$

11.

A graph of cos(2x). Graph has amplitude of 1, period of pi, and range of [-1,1].

amplitude: 1; period: $\pi$ ; midline: $y=0$ ; maximum: $y=1$ occurs at $x=\pi$ ; minimum: $y=-1$ occurs at $x=\frac{\pi}{2}$ ; one full period is graphed from $x=0$ to $x=\pi$

13.

A graph of 4cos(pi*x). Grpah has amplitude of 4, period of 2, and range of [-4, 4].

amplitude: 4; period: 2; midline: $y=0$ ; maximum: $y=4$ occurs at $x=0$ ; minimum: $y=-4$ occurs at $x=1$

15.

A graph of 3sin(8(x+4))+5. Graph has amplitude of 3, range of [2, 8], and period of pi/4. — A graph of 3sin(8(x+4))+5. Graph has amplitude of 3, range of [2, 8], and period of pi/4].

amplitude: 3; period: $\frac{\pi}{4}$ ; midline: $y=5$ ; maximum: $y=8$ occurs at $x=0.12$ ; minimum: $y=2$ occurs at $x=0.516$ ; horizontal shift: $-4$ ; vertical translation 5; one period occurs from $x=0$ to $x=\frac{\pi}{4}$

17.

A graph of 5sin(5x+20)-2. Graph has an amplitude of 5, period of 2pi/5, and range of [-7,3].

amplitude: 5; period: $\frac{2\pi}{5}$ ; midline: $y=-2$ ; maximum: $y=3$ occurs at $x=0.08$ ; minimum: $y=-7$ occurs at $x=0.71$ ; phase shift: $-4$ ; vertical translation: $-2$ ; one full period can be graphed on $x=0$ to $x=\frac{2\pi}{5}$

19.

A graph of -cos(t+pi/3)+1. Graph has amplitude of 1, period of 2pi, and range of [0,2]. Phase shifted pi/3 to the left.

amplitude: 1 ; period: $2\pi$ ; midline: $y=1$ ; maximum: $y=2$ occurs at $x=2.09$ ; maximum: $y=2$ occurs at $t=2.09$ ; minimum: $y=0$ occurs at $t=5.24$ ; phase shift: $-\frac{\pi}{3}$ ; vertical translation: 1; one full period is from $t=0$ to $t=2\pi$

21.

A graph of -sin((1/2)*t + 5pi/3). Graph has amplitude of 1, range of [-1,1], period of 4pi, and a phase shift of -10pi/3.

amplitude: 1; period: $4\pi$ ; midline: $y=0$ ; maximum: $y=1$ occurs at $t=11.52$ ; minimum: $y=-1$ occurs at $t=5.24$ ; phase shift: $-\frac{10\pi}{3}$ ; vertical shift: 0

23. amplitude: 2; midline: $y=-3$ ; period: 4; equation: $f(x)=2\sin(\frac{\pi}{2}x)-3$

25. amplitude: 2; period: 5; midline: $y=3$ ; equation: $f(x)=-2\cos(\frac{2\pi}{5}x)+3$

27. amplitude: 4; period: 2; midline: $y=0$ ; equation: $f(x)=-4\cos(\pi(x-\frac{\pi}{2}))$

29. amplitude: 2; period: 2; midline $y=1$ ; equation: $f(x)=2\cos(\pi x)+1$

31. $0,\pi$

33. $\sin(\frac{\pi}{2})=1$

35. $\frac{\pi}{2}$

37. $f(x)=\sin x$ is symmetric

39. $\frac{\pi}{3},\frac{5\pi}{3}$

41. Maximum: 1 at $x=0$ ; minimum: -1 at $x=\pi$

43. A linear function is added to a periodic sine function. The graph does not have an amplitude because as the linear function increases without bound the combined function $h(x)=x+\sin x$ will increase without bound as well. The graph is bounded between the graphs of $y=x+1$ and $y=x-1$ because sine oscillates between −1 and 1.

45. There is no amplitude because the function is not bounded.

47. The graph is symmetric with respect to the y-axis and there is no amplitude because the function’s bounds decrease as $| x |$ grows. There appears to be a horizontal asymptote at $y=0$ .

8.2 Section Exercises

1. Since $y=\csc x$ is the reciprocal function of $y=\sin x,$ you can plot the reciprocal of the coordinates on the graph of $y=\sin x$ to obtain the y-coordinates of $y=\csc x.$ The x-intercepts of the graph $y=\sin x$ are the vertical asymptotes for the graph of $y=\csc x.$

3. Answers will vary. Using the unit circle, one can show that $\tan(x+\pi)=\tan x.$

5. The period is the same: $2\pi.$

7. IV

9. III

11. period: 8; horizontal shift: 1 unit to left

13. 1.5

15. 5

17. $-\cot x \cos x-\sin x$

19.

A graph of two periods of a modified tangent function. There are two vertical asymptotes.

stretching factor: 2; period: $\frac{\pi}{4}$ ; asymptotes: $x=\frac{1}{4}(\frac{\pi}{2}+\pi k)+8,$ where k is an integer

21.

A graph of two periods of a modified cosecant function. Vertical Asymptotes at x= -6, -3, 0, 3, and 6.

stretching factor: 6; period: 6; asymptotes: $x=3k,$ where k is an integer

23.

A graph of two periods of a modified tangent function. Vertical asymptotes at multiples of pi.

stretching factor: 1; period: $\pi$ ; asymptotes: $x=\pi k,$ where k is an integer

25.

A graph of two periods of a modified tangent function. Three vertical asymptiotes shown.

Stretching factor: 1; period: $\pi$ ; asymptotes: $x=\frac{\pi}{4}+\pi k,$ where k is an integer

27.

A graph of two periods of a modified cosecant function. Vertical asymptotes at multiples of pi.

stretching factor: 2; period: $2\pi$ ; asymptotes: $x=\pi k,$ where k is an integer

29.

A graph of two periods of a modified secant function. Vertical asymptotes at x=-pi/2, -pi/6, pi/6, and pi/2.

stretching factor: 4; period: $\frac{2\pi}{3}$ ; asymptotes: $x=\frac{\pi}{6}k,$ where k is an odd integer

31.

A graph of two periods of a modified secant function. There are four vertical asymptotes all pi/5 apart.

stretching factor: 7; period: $\frac{2\pi}{5}$ ; asymptotes: $x=\frac{\pi}{10}k,$ where k is an odd integer

33.

A graph of two periods of a modified cosecant function. Three vertical asymptotes, each pi apart.

stretching factor: 2; period: $2\pi$ ; asymptotes: $x=-\frac{\pi}{4}+\pi k,$ where k is an integer

35.

A graph of a modified cosecant function. Four vertical asymptotes.

stretching factor: $\frac{7}{5}$ ; period: $2\pi$ ; asymptotes: $x=\frac{\pi}{4}+\pi k,$ where k is an integer

37. $y=\tan(3(x-\frac{\pi}{4}))+2$

A graph of two periods of a modified tangent function. Vertical asymptotes at x=-pi/4 and pi/12.

39. $f(x)=\csc(2x)$

41. $f(x)=\csc(4x)$

43. $f(x)=2\csc x$

45. $f(x)=\frac{1}{2}\tan(100\pi x)$

47.

A graph of the absolute value of the cotangent function. Range is 0 to infinity.

49.

51.

A graph of two periods of a modified secant function. Vertical asymptotes at multiples of 500pi.

53.

55.

$(-\frac{\pi}{2},\frac{\pi}{2})$ ;
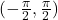A graph of a half period of a secant function. Vertical asymptotes at x=-pi/2 and pi/2.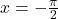
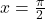$x=-\frac{\pi}{2}$ and $x=\frac{\pi}{2}$ ; the distance grows without bound as 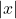$| x |$ approaches 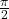$\frac{\pi}{2}$ —i.e., at right angles to the line representing due north, the boat would be so far away, the fisherman could not see it;
3; when 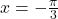$x=-\frac{\pi}{3}$ , the boat is 3 km away;
1.73; when 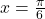$x=\frac{\pi}{6}$ , the boat is about 1.73 km away;
1.5 km; when $x=0$

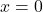
57.

$h(x)=2\tan(\frac{\pi}{120}x)$ ;
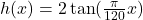An exponentially increasing function with a vertical asymptote at x=60.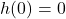
$h(0)=0$ : after 0 seconds, the rocket is 0 mi above the ground; 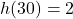$h(30)=2$ : after 30 seconds, the rockets is 2 mi high;
As 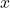$x$ approaches 60 seconds, the values of 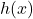$h(x)$ grow increasingly large. The distance to the rocket is growing so large that the camera can no longer track it.

8.3 Section Exercises

1. The function $y=\sin x$ is one-to-one on $[-\frac{\pi}{2},\frac{\pi}{2}]$ ; thus, this interval is the range of the inverse function of $y=\sin x,$ $f(x)=\sin^{-1}x.$ The function $y=\cos x$ is one-to-one on $[0,\pi]$ ; thus, this interval is the range of the inverse function of $y=\cos x, f(x)=\cos^{-1}x.$

3. $\frac{\pi}{6}$ is the radian measure of an angle between $-\frac{\pi}{2}$ and $\frac{\pi}{2}$ whose sine is 0.5.

5. In order for any function to have an inverse, the function must be one-to-one and must pass the horizontal line test. The regular sine function is not one-to-one unless its domain is restricted in some way. Mathematicians have agreed to restrict the sine function to the interval $[-\frac{\pi}{2},\frac{\pi}{2}]$ so that it is one-to-one and possesses an inverse.

7. True . The angle, $\theta_1$ that equals $\arccos(-x)$ , $x>0$ , will be a second quadrant angle with reference angle, $\theta_2$ , where $\theta_2$ equals $\arccos x$ , $x>0$ . Since $\theta_2$ is the reference angle for $\theta_1$ , $\theta_2=\pi-\theta_1$ and $\arccos(-x)$ = $\pi-\arccos x$ –

9. $-\frac{\pi}{6}$

11. $\frac{3\pi}{4}$

13. $-\frac{\pi}{3}$

15. $\frac{\pi}{3}$

17. 1.98

19. 0.93

21. 1.41

23. 0.56 radians

25. 0

27. 0.71

29. -0.71

31. $-\frac{\pi}{4}$

33. 0.8

35. $\frac{5}{13}$

37. $\frac{x-1}{\sqrt{-x^2+2x}}$

39. $\frac{\sqrt{x^2-1}}{x}$

41. $\frac{x+0.5}{\sqrt{-x^2-x+\frac{3}{4}}}$

43. $\frac{\sqrt{2x+1}}{x+1}$

45. $\frac{\sqrt{2x+1}}{x}$

47. $t$

49.

A graph of the function arc cosine of x over -1 to 1. The range of the function is 0 to pi.

domain $[-1,1];$ range $[0,\pi]$

51. approximately $x=0.00$

53. 0.395 radians

55. 1.11 radians

57. 1.25 radians

59. 0.405 radians

61. No. The angle the ladder makes with the horizontal is 60 degrees.

Review Exercises

1. amplitude: 3; period: $2\pi$ ; midline: $y=3$ ; no asymptotes

A graph of two periods of a function with a cosine parent function. The graph has a range of [0,6] graphed over -2pi to 2pi. Maximums as -pi and pi.

3. amplitude: 3; period: $2\pi$ ; midline: $y=0$ ; no asymptotes

A graph of four periods of a function with a cosine parent function. Graphed from -4pi to 4pi. Range is [-3,3].

5. amplitude: 3; period: $2\pi$ ; midline: $y=-4$ ; no asymptotes

A graph of two periods of a sinusoidal function. Range is [-7,-1]. Maximums at -5pi/4 and 3pi/4.

7. amplitude: 6; period: $\frac{2\pi}{3}$ ; midline: $y=-1$ ; no asymptotes

A sinusoidal graph over two periods. Range is [-7,5], amplitude is 6, and period is 2pi/3.

9. stretching factor: none; period: $\pi$ ; midline: $y=-4$ ; asymptotes: $x=\frac{\pi}{2}+\pi k,$ where $k$ is an integer

A graph of a tangent function over two periods. Graphed from -pi to pi, with asymptotes at -pi/2 and pi/2.

11. stretching factor: 3; period: $\frac{\pi}{4}$ ; midline: $y=-2$ ; asymptotes: $x=\frac{\pi}{8}+\frac{\pi}{4}k,$ where $k$ is an integer

A graph of a tangent function over two periods. Asymptotes at -pi/8 and pi/8. Period of pi/4. Midline at y=-2.

13. amplitude: none; period: $2\pi$ ; no phase shift; asymptotes: $x=\frac{\pi}{2}k,$ where $k$ is an odd integer

A graph of two periods of a secant function. Period of 2 pi, graphed from -2pi to 2pi. Asymptotes at -3pi/2, -pi/2, pi/2, and 3pi/2.

15. amplitude: none; period: $\frac{2\pi}{5}$ ; no phase shift; asymptotes: $x=\frac{\pi}{5}k,$ where $k$ is an integer

A graph of a cosecant functionover two and a half periods. Graphed from -pi to pi, period of 2pi/5.

17. amplitude: none; period: $4\pi$ ; no phase shift; asymptotes: $x=2\pi k,$ where $k$ is an integer

A graph of two periods of a cosecant function. Graphed from -4pi to 4pi. Asymptotes at multiples of 2pi. Period of 4pi.

19. largest: 20,000; smallest: 4,000

21. amplitude: 8,000; period: 10; phase shift: 0

23. In 2007, the predicted population is 4,413. In 2010, the population will be 11,924.

25. 5 in.

27. 10 seconds

29. $\frac{\pi}{6}$

31. $\frac{\pi}{4}$

33. $\frac{\pi}{3}$

35. No solution

37. $\frac{12}{5}$

39. The graphs are not symmetrical with respect to the line $y=x.$ They are symmetrical with respect to the $y$ -axis.

A graph of cosine of x and secant of x. Cosine of x has maximums where secant has minimums and vice versa. Asymptotes at x=-3pi/2, -pi/2, pi/2, and 3pi/2.

41. The graphs appear to be identical.

Two graphs of two identical functions on the interval [-1 to 1]. Both graphs appear sinusoidal.

Practice Test

1. amplitude: 0.5; period: $2\pi$ ; midline $y=0$

A graph of two periods of a sinusoidal function, graphed over -2pi to 2pi. The range is [-0.5,0.5]. X-intercepts at multiples of pi.

3. amplitude: 5; period: $2\pi$ ; midline: $y=0$

Two periods of a sine function, graphed over -2pi to 2pi. The range is [-5,5], amplitude of 5, period of 2pi.

5. amplitude: 1; period: $2\pi$ ; midline: $y=1$

A graph of two periods of a cosine function, graphed over -7pi/3 to 5pi/3. Range is [0,2], Period is 2pi, amplitude is1.

7. amplitude: 3; period: $6\pi$ ; midline: $y=0$

A graph of two periods of a cosine function, over -7pi/2 to 17pi/2. The range is [-3,3], period is 6pi, and amplitude is 3.

9. amplitude: none; period: $\pi$ ; midline: $y=0,$ asymptotes: $x=\frac{2\pi}{3}+\pi k,$ where $k$ is an integer

A graph of two periods of a tangent function over -5pi/6 to 7pi/6. Period is pi, midline at y=0.

11. amplitude: none; period: $\frac{2\pi}{3}$ ; midline: $y=0,$ asymptotes: $x=\frac{\pi}{3}k,$ where $k$ is an integer

A graph of two periods of a cosecant functinon, over -2pi/3 to 2pi/3. Vertical asymptotes at multiples of pi/3. Period of 2pi/3.

13. amplitude: none; period: $2\pi$ ; midline: $y=-3$

A graph of two periods of a cosecant function, graphed from -9pi/4 to 7pi/4. Period is 2pi, midline at y=-3.

15. amplitude: 2; period: 2; midline: $y=0$ ; $f(x)=2\sin(\pi(x-1))$

17. amplitude: 1; period: 12; phase shift: $-6$ ; midline $y=-3$

19. $D(t)=68-12\sin(\frac{\pi}{12}x)$

21. period: $\frac{\pi}{6}$ ; horizontal shift: $-7$

23. $f(x)=\sec(\pi x)$ ; period: 2; phase shift: 0

25. 4

27. The views are different because the period of the wave is $\frac{1}{25}$ . Over a bigger domain, there will be more cycles of the graph.

Two side-by-side graphs of a sinusodial function. The first graph is graphed over 0 to 1, the second graph is graphed over 0 to 3. There are many periods for each.

29. $\frac{3}{5}$

31. On the approximate intervals $(0.5,1),(1.6,2.1),(2.6,3.1),(3.7,4.2),(4.7,5.2),(5.6,6.28)$

33. $f(x)=2\cos(12(x+\frac{\pi}{4}))+3$

A graph of one period of a cosine function, graphed over -pi/4 to 0. Range is [1,5], period is pi/6.

35. This graph is periodic with a period of $2\pi$ .

A graph of two periods of a sinusoidal function, The graph has a period of 2pi.

37. $\frac{\pi}{3}$

39. $\frac{\pi}{2}$

41. $\sqrt{1-(1-2x)^2}$

43. $\frac{1}{\sqrt{1+\frac{x}{4}}}$

45. $\frac{\sqrt{x+1}}{x}$

47. False

49. approximately 0.07 radians

Answer Key Chapter 8 – Algebra and Trigonometry 2e | OpenStax

Try It

8.1 Graphs of the Sine and Cosine Functions

8.2 Graphs of the Other Trigonometric Functions

8.3 Inverse Trigonometric Functions

8.1 Section Exercises

8.2 Section Exercises

8.3 Section Exercises

Review Exercises

Practice Test

License

Share This Book