Ch. 6 Review Exercises
Chapter Test
- Determine whether the following collection describes a well-defined set: “A group of small tomatoes.”
- Classify each of the following sets as either finite or infinite.
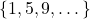
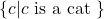

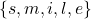
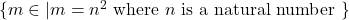
- Use the sets provided to answer the following questions:
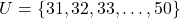 ,
, 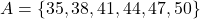 ,
, 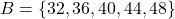 , and
, and 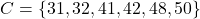 .
. - Find
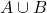 .
. - Find
 .
. - Determine if set
 is equivalent to, equal to, or neither equal nor equivalent to set
is equivalent to, equal to, or neither equal nor equivalent to set 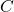 . Justify your answer.
. Justify your answer. - Find
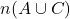 .
. - Find
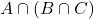 .
. - Find
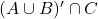 .
. - Find
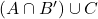 .<
.<
Review Exercises
Exponential Functions
- Determine whether the function
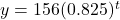 represents exponential growth, exponential decay, or neither. Explain
represents exponential growth, exponential decay, or neither. Explain - The population of a herd of deer is represented by the function
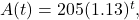 where
where 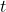 is given in years. To the nearest whole number, what will the herd population be after
is given in years. To the nearest whole number, what will the herd population be after 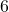 years?
years? - Find an exponential equation that passes through the points
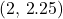 and
and 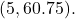
- Determine whether Table 1 could represent a function that is linear, exponential, or neither. If it appears to be exponential, find a function that passes through the points.
x 1 2 3 4 f(x) 3 0.9 0.27 0.081 - A retirement account is opened with an initial deposit of $8,500 and earns
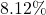 interest compounded monthly. What will the account be worth in
interest compounded monthly. What will the account be worth in 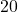 years?
years? - Hsu-Mei wants to save $5,000 for a down payment on a car. To the nearest dollar, how much will she need to invest in an account now with
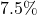 APR, compounded daily, in order to reach her goal in
APR, compounded daily, in order to reach her goal in 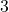 years?
years? - Does the equation
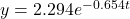 represent continuous growth, continuous decay, or neither? Explain.
represent continuous growth, continuous decay, or neither? Explain. - Suppose an investment account is opened with an initial deposit of
 earning
earning 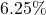 interest, compounded continuously. How much will the account be worth after
interest, compounded continuously. How much will the account be worth after 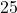 years?
years?
Graphs of Exponential Functions
- Graph the function
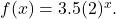 State the domain and range and give the y-intercept.
State the domain and range and give the y-intercept. - Graph the function
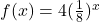 and its reflection about the y-axis on the same axes, and give the y-intercept.
and its reflection about the y-axis on the same axes, and give the y-intercept. - The graph of
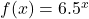 is reflected about the y-axis and stretched vertically by a factor of
is reflected about the y-axis and stretched vertically by a factor of 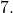 What is the equation of the new function,
What is the equation of the new function, 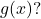 State its y-intercept, domain, and range.
State its y-intercept, domain, and range. - The graph below shows transformations of the graph of
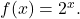 What is the equation for the transformation?
What is the equation for the transformation?
Figure 1
Logarithmic Functions
- Rewrite
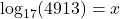 as an equivalent exponential equation.
as an equivalent exponential equation. - Rewrite
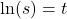 as an equivalent exponential equation.
as an equivalent exponential equation. - Rewrite
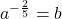 as an equivalent logarithmic equation.
as an equivalent logarithmic equation. - Rewrite
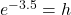 as an equivalent logarithmic equation.
as an equivalent logarithmic equation. - Solve for x if
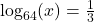 by converting the logarithmic equation
by converting the logarithmic equation 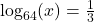 to exponential form.
to exponential form. - Evaluate
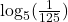 without using a calculator.
without using a calculator. - Evaluate
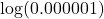 without using a calculator.
without using a calculator. - Evaluate
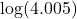 using a calculator. Round to the nearest thousandth.
using a calculator. Round to the nearest thousandth. - Evaluate
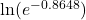 without using a calculator.
without using a calculator. - Evaluate
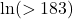 using a calculator. Round to the nearest thousandth.
using a calculator. Round to the nearest thousandth.
Graphs of Logarithmic Functions
- Graph the function
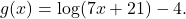
- Graph the function
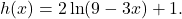
- State the domain, vertical asymptote, and end behavior of the function
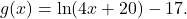
Logarithmic Properties
- Rewrite
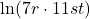 in expanded form.
in expanded form. - Rewrite
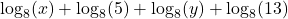 in compact form.
in compact form. - Rewrite
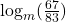 in expanded form.
in expanded form. - Rewrite
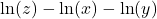 in compact form.
in compact form. - Rewrite
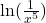 as a product.
as a product. - Rewrite
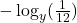 as a single logarithm.
as a single logarithm. - Use properties of logarithms to expand
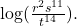
- Use properties of logarithms to expand
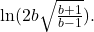
- Condense the expression
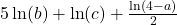 to a single logarithm.
to a single logarithm. - Condense the expression
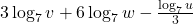 to a single logarithm.
to a single logarithm. - Rewrite
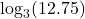 to base
to base 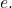
- Rewrite
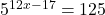 as a logarithm. Then apply the change of base formula to solve for
as a logarithm. Then apply the change of base formula to solve for 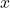 using the common log. Round to the nearest thousandth.
using the common log. Round to the nearest thousandth.
Exponential and Logarithmic Equations
- Solve
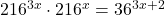 by rewriting each side with a common base.
by rewriting each side with a common base. - Solve
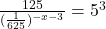 by rewriting each side with a common base.
by rewriting each side with a common base. - Use logarithms to find the exact solution for
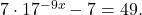 If there is no solution, write no solution.
If there is no solution, write no solution. - Use logarithms to find the exact solution for
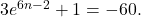 If there is no solution, write no solution.
If there is no solution, write no solution. - Find the exact solution for
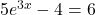 . If there is no solution, write no solution.
. If there is no solution, write no solution. - Find the exact solution for
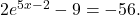 If there is no solution, write no solution.
If there is no solution, write no solution. - Find the exact solution for
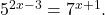 If there is no solution, write no solution.
If there is no solution, write no solution. - Find the exact solution for
 If there is no solution, write no solution.
If there is no solution, write no solution. - Use the definition of a logarithm to solve.
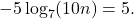
- Use the definition of a logarithm to find the exact solution for
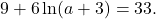
- Use the one-to-one property of logarithms to find an exact solution for
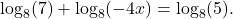 If there is no solution, write no solution.
If there is no solution, write no solution. - Use the one-to-one property of logarithms to find an exact solution for
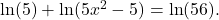 If there is no solution, write no solution.
If there is no solution, write no solution. - The formula for measuring sound intensity in decibels
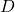 is defined by the equation
is defined by the equation 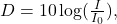 where
where 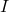 is the intensity of the sound in watts per square meter and
is the intensity of the sound in watts per square meter and 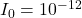 is the lowest level of sound that the average person can hear. How many decibels are emitted from a large orchestra with a sound intensity of
is the lowest level of sound that the average person can hear. How many decibels are emitted from a large orchestra with a sound intensity of 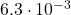 watts per square meter?
watts per square meter? - The population of a city is modeled by the equation
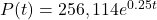 where
where 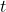 is measured in years. If the city continues to grow at this rate, how many years will it take for the population to reach one million?
is measured in years. If the city continues to grow at this rate, how many years will it take for the population to reach one million? - Find the inverse function
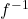 for the exponential function
for the exponential function 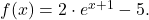
- Find the inverse function
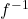 for the logarithmic function
for the logarithmic function 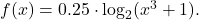
Exponential and Logarithmic Models
For the following exercises, use this scenario: A doctor prescribes
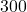 milligrams of a therapeutic drug that decays by about
milligrams of a therapeutic drug that decays by about 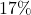 each hour.
each hour.- To the nearest minute, what is the half-life of the drug?
- Write an exponential model representing the amount of the drug remaining in the patient’s system after
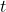 hours. Then use the formula to find the amount of the drug that would remain in the patient’s system after
hours. Then use the formula to find the amount of the drug that would remain in the patient’s system after 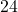 hours. Round to the nearest hundredth of a gram.
hours. Round to the nearest hundredth of a gram.
For the following exercises, use this scenario: A soup with an internal temperature of
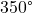 Fahrenheit was taken off the stove to cool in a
Fahrenheit was taken off the stove to cool in a 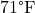 room. After fifteen minutes, the internal temperature of the soup was
room. After fifteen minutes, the internal temperature of the soup was 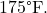
- Use Newton’s Law of Cooling to write a formula that models this situation.
- How many minutes will it take the soup to cool to
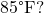
For the following exercises, use this scenario: The equation
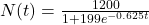 models the number of people in a school who have heard a rumor after
models the number of people in a school who have heard a rumor after 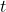 days.
days.- How many people started the rumor?
- To the nearest tenth, how many days will it be before the rumor spreads to half the carrying capacity?
- What is the carrying capacity?
For the following exercises, enter the data from each table into a graphing calculator and graph the resulting scatter plots. Determine whether the data from the table would likely represent a function that is linear, exponential, or logarithmic.
-
x f(x) 1 3.05 2 4.42 3 6.4 4 9.28 5 13.46 6 19.52 7 28.3 8 41.04 9 59.5 10 86.28 -
x f(x) 0.5 18.05 1 17 3 15.33 5 14.55 7 14.04 10 13.5 12 13.22 13 13.1 15 12.88 17 12.69 20 12.45 - Find a formula for an exponential equation that goes through the points
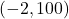 and
and 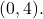 Then express the formula as an equivalent equation with base e.
Then express the formula as an equivalent equation with base e.
Fitting Exponential Models to Data
- What is the carrying capacity for a population modeled by the logistic equation
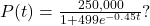 What is the initial population for the model?
What is the initial population for the model? - The population of a culture of bacteria is modeled by the logistic equation
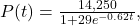 where
where 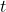 is in days. To the nearest tenth, how many days will it take the culture to reach
is in days. To the nearest tenth, how many days will it take the culture to reach 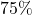 of its carrying capacity?
of its carrying capacity?
For the following exercises, use a graphing utility to create a scatter diagram of the data given in the table. Observe the shape of the scatter diagram to determine whether the data is best described by an exponential, logarithmic, or logistic model. Then use the appropriate regression feature to find an equation that models the data. When necessary, round values to five decimal places.
-
x f(x) 1 409.4 2 260.7 3 170.4 4 110.6 5 74 6 44.7 7 32.4 8 19.5 9 12.7 10 8.1 -
x f(x) 0.15 36.21 0.25 28.88 0.5 24.39 0.75 18.28 1 16.5 1.5 12.99 2 9.91 2.25 8.57 2.75 7.23 3 5.99 3.5 4.81 -
x f(x) 0 9 2 22.6 4 44.2 5 62.1 7 96.9 8 113.4 10 133.4 11 137.6 15 148.4 17 149.3
/li>
- Determine whether the function
- Use the Venn diagram below to answer the following questions.
Figure [Number] A two-set Venn diagram of A and B is given. Set A shows e, l while set B shows g. The intersection of the sets shows o, d. Outside sets A and B, n is shown. The union of the sets A and B shows (g, o, l, d, e, n). - Find
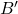 .
. - Find
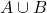 .
. - Find
 .
. - Draw a Venn diagram to represent the relationship between the two sets: “All flowers are plants.”
- For the following questions, use the Venn diagram showing the blood types of all donors at a recent mobile blood drive.
Figure [Number] A three-set Venn diagram of A, B, and Rh plus overlapping one another is given. The total number of donors equals 128. Set A shows 7; Set B shows 5; Set Rh plus shows 47. Overlapping of sets A and B shows 4, overlapping of sets B and Rh plus shows 12, and overlapping of A and Rh plus shows 40. Overlapping of A, B, and Rh plus shows 3. - Find the number of donors who were
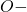 ; that is, find
; that is, find 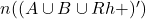 .
. - Find the number of donors who were
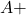 or
or 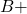 or
or 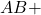 .
. - Use Venn diagrams to prove that if
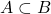 , then
, then 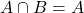 .
.
Attribution
Text Attribution
This text was adapted from Chapter 1 of Contemporary Mathematics, textbooks originally published by OpenStax.
