2.5 Chapter 2 Review
Chapter Review
The Multiplication Rule for Counting
- You are booking a round trip flight for vacation. If there are 4 outbound flight options and 7 return flight options, how many different options do you have?
- You are putting together a social committee for your club. You’d like broad representation, so you will choose one person from each class. If there are 8 seniors, 12 juniors, 10 sophomores, and 6 first-years, how many committees are possible?
- The Big Breakfast Platter at Jimbo’s Sausage Haus gives you your choice of 4 flavors of sausage, 5 preparations for eggs, 3 different potato options, and 4 different breads. If you choose one of each, how many different Big Breakfast Platters can be selected?
- The multiple-choice quiz you’re about to take has 10 questions with 4 choices for each. How many ways are there to fill out the quiz?
Permutations
- Compute
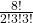 .
. - Compute
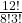 .
. - Compute
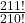 .
. - Compute
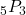 .
. - Compute
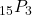 .
. - Compute
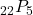 .
. - As you plan your day, you see that you have 6 tasks on your to-do list. You’ll only have time for 5 of those. How many schedules are possible for you today?
- As captain of your intramural softball team, you are responsible for setting the 10-person batting order for the team. If there are 12 people on the team, how many batting orders are possible?
Combinations
- If you’re trying to decide which 4 of your 12 friends to invite to your apartment for a dinner party, are you using permutations or combinations?
- If you’re trying to decide which of your guests sits where at your table, are you using permutations or combinations?
- Compute
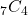 .
. - Compute
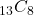 .
. - How many ways are there to draw a hand of 8 cards from a deck of 16 cards?
- In a card game with 4 players and a deck of 12 cards, how many ways are there to deal out the four 3-card hands?
Each of the following exercises involve drawing a Scrabble tile from a bag. These tiles are labeled with a letter and a point value, as follows: A(1), C(3), D(2), E(1), E(1), J(8), K(5), O(1), R(1), R(1).
- How many ways are there to draw a vowel and then a consonant from the bag?
- How many ways are there to draw a tile worth an even number of points and then a tile worth an odd number of points from the bag?
- How many ways are there to draw 4 tiles from the bag without replacement, if order matters?
- How many ways are there to draw 4 consonants from the bag without replacement, if order matter?
- How many ways are there to draw 4 tiles from the bag with replacement, if order does not matter?
- How many ways are there to draw 4 consonants from the bag with replacement, if order does not matter?
- Give the sample space of the experiment that asks you to draw 2 tiles from the bag with replacement and note their point values, where order doesn’t matter. Give the outcomes as ordered pairs.
- Give the sample space of the experiment that asks you to draw 2 tiles from the bag without replacement and note their point values, where order doesn’t matter. Give the outcomes as ordered pairs.
- If you draw a single tile from the bag, what is the probability that it’s an E?
- If you draw a single tile from the bag, what is the probability that it’s not an A?
- If you draw 3 tiles from the bag without replacement, what is the probability that they spell RED, in order?
- If you draw 3 tiles from the bag without replacement, what is the probability that they spell RED, in any order?
- What are the odds against drawing a vowel?
- Use your answer to question 12 to find the odds against drawing three tiles without replacement and being able to spell RED.
- If you draw one tile, what is the probability of drawing a J or a K?
- If you draw one tile, what is the probability that it’s a vowel or that it’s worth more than 4 points?
- Suppose you’re about to draw one tile from the bag. Find
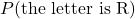 and
and 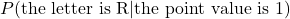 .
. - If you draw 2 tiles with replacement, what is the probability of drawing a consonant first and then a vowel?
- If you draw 2 tiles without replacement, what is the probability of drawing a consonant first and then a vowel?
- If you draw 10 tiles with replacement, what is the probability that you draw exactly 3 vowels? Round to 3 decimal places.
- If you draw 100 tiles with replacement, what is the probability that you draw fewer than 35 vowels? Round to 4 decimal places.
- Find and interpret the expected number of points on the tile, assuming you draw 1 tile from the bag.
- Find the expected sum of points on 2 tiles, selected without replacement.
- If your friend offers you a bet where they pay you $10 if you draw a vowel from the bag, but you owe them $5 if you draw a consonant, should you take it? How do you know?
Attribution
Text Attribution
This text was adapted from Chapter 7 of Contemporary Mathematics, textbooks originally published by OpenStax.
