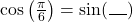Ch. 7 Practice Test – Algebra and Trigonometry 2e | OpenStax
Practice Test
-
Convert
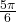 radians to degrees.
radians to degrees. -
Convert
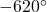 to radians.
to radians. -
Find the length of a circular arc with a radius 12 centimeters subtended by the central angle of
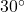 .
. -
Find the area of the sector with radius of 8 feet and an angle of
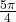 radians.
radians. -
Find the angle between
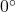 and
and 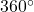 that is coterminal with
that is coterminal with 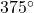 .
. -
Find the angle between 0 and
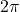 in radians that is coterminal with
in radians that is coterminal with 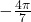 .
. -
Draw the angle
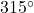 in standard position on the Cartesian plane.
in standard position on the Cartesian plane. -
Draw the angle
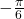 in standard position on the Cartesian plane.
in standard position on the Cartesian plane. -
A carnival has a Ferris wheel with a diameter of 80 feet. The time for the Ferris wheel to make one revolution is 75 seconds. What is the linear speed in feet per second of a point on the Ferris wheel? What is the angular speed in radians per second?
-
Find the missing sides of the triangle
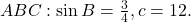
-
Find the missing sides of the triangle.
-
The angle of elevation to the top of a building in Chicago is found to be 9 degrees from the ground at a distance of 2000 feet from the base of the building. Using this information, find the height of the building.
-
Find the exact value of
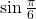 .
. -
Compute sine of
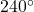 .
. -
State the domain of the sine and cosine functions.
-
State the range of the sine and cosine functions.
-
Find the exact value of
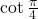 .
. -
Find the exact value of
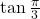 .
. -
Use reference angles to evaluate
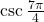 .
. -
Use reference angles to evaluate
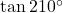 .
. -
If
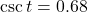 , what is the
, what is the 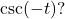
-
If
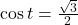 , find
, find 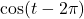 .
. -
Find the missing angle: